Nesta aula, exploraremos como avaliar se um modelo de regressão linear é bom, incluindo métricas de desempenho, testes estatísticos e análise de resíduos. Além disso, veremos exercícios práticos com tabelas de dados para calcular regressões e interpretar resultados.A regressão linear é uma técnica estatística que modela a relação entre uma variável dependente (Y) e uma variável independente (X). Mas como sabemos se o modelo é confiável? Para isso, precisamos avaliar sua qualidade por meio de indicadores estatísticos.Indicadores de Qualidade de uma Regressão Linear Análise dos ResíduosOs resíduos são os erros do modelo:\[ \text{Resíduo} = y_i - \hat{y}_i \]Para um bom modelo, os resíduos devem:1. Ser aleatórios (sem padrões claros).2. Ter média zero (sem viés sistemático).3. Ter variância constante (homocedasticidade).4. Seguir distribuição normal (para inferência válida).Como avaliar os resíduos?MétodoO que verificar?Gráfico Resíduos vs. 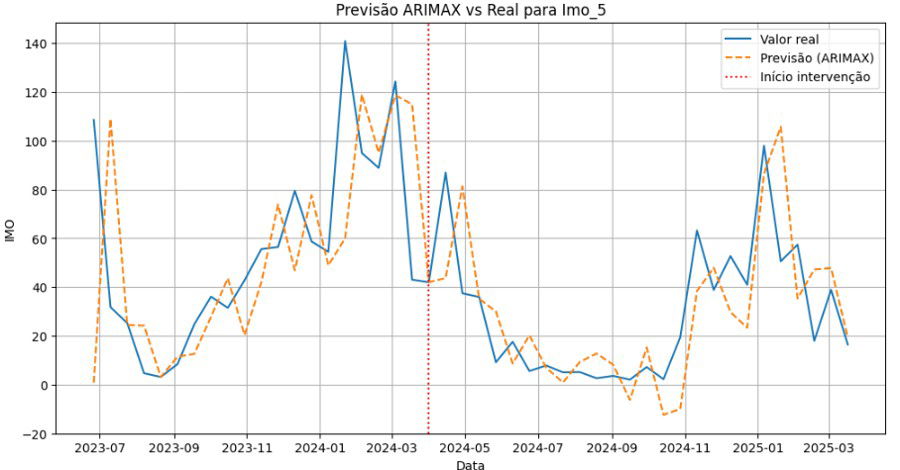PrevistosSe há padrões (curvas, funis)Histograma dos ResíduosSe a distribuição é normalGráfico Q-QSe os resíduos seguem a normalidadeProblemas comuns:- Heterocedasticidade: Variância não constante (gráfico em "funil").- Não normalidade: Resíduos distorcidos (afeta testes estatísticos).- Autocorrelação: Padrões temporais (em séries temporais).Exemplo de uma regressão boa:Regressão bem ajustadaExemplo de resíduo bom:Resíduo bom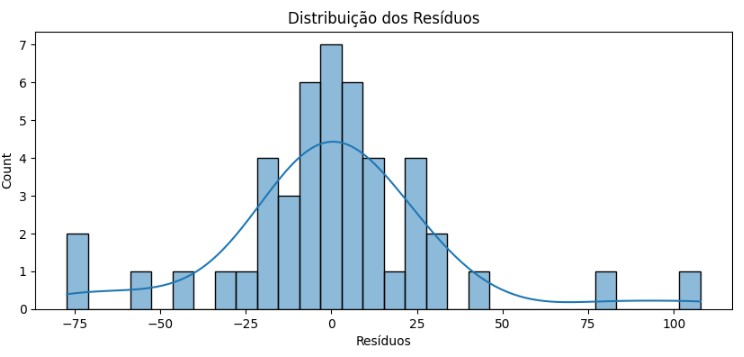Repare que aqui podemos usar conceitos como Curtose e Assimetria para garantir que os resíduos possuem formatos mais interessantes como "Simétrica" e "Mesocúrtica".Erro Padrão da Estimativa (SEE)SEE (Standard Error of the Estimate ou Erro Padrão da Estimativa, em português) mede o erro médio que o modelo comete ao prever Y.Fórmula:\[ SEE = \sqrt{\frac{\sum (y_i - \hat{y}_i)^2}{n - 2}} \]- Quanto menor o SEE, mais preciso o modelo.- Útil para comparar modelos diferentes.Teste t e Valor-pO teste t verifica se o coeficiente angular (β₁) é estatisticamente significativo.Hipóteses:- \( H_0: \beta_1 = 0 \) (não há relação)- \( H_1: \beta_1 \neq 0 \) (há relação)Interpretação do p-valor:- p < 0,05: Rejeita \( H_0 \) (relação significativa).- p > 0,05: Não rejeita \( H_0 \) (sem evidência de relação).Intervalo de Confiança para os CoeficientesO IC 95% para \( \beta_1 \) mostra a faixa de valores plausíveis.- Se não inclui zero, há relação significativa.Coeficiente de Determinação (R²)O R² (coeficiente de determinação) mede quanto da variação de Y é explicada por X.Fórmula:\[ R^2 = \frac{SQ_{\text{Regressão}}}{SQ_{\text{Total}}} \]Onde:- \( SQ_{\text{Regressão}} \) = Soma dos Quadrados da Regressão- \( SQ_{\text{Total}} \) = Soma dos Quadrados TotalOu\[ R^2 = 1 - \frac{SEE}{SQ_{\text{Total}}} \]Interpretação:- 0 ≤ R² ≤ 1 (quanto mais próximo de 1, melhor).- Se \( R^2 = 0,75 \), significa que 75% da variação de Y é explicada por X.Limitações do R²:- Não indica causalidade (apenas associação).- Pode ser enganoso se houver muitos outliers ou relações não lineares.Exemplo Prático com Tabela de DadosVamos analisar uma regressão entre horas de estudo (X) e nota na prova (Y).AlunoHoras (X)Nota (Y)125024603680487051090Passos para calcular a regressão:1. Calcular \( \hat{Y} = \beta_0 + \beta_1 X \)2. Avaliar R², SEE e p-valor3. Analisar resíduosPasso 1: Calcular a Regressão Linear(\(\hat{Y} = \beta_0 + \beta_1 X\))Precisamos encontrar \(\beta_0\) (intercepto) e \(\beta_1\) (inclinação).Fórmulas:\[\beta_1 = \frac{n \sum XY - (\sum X)(\sum Y)}{n \sum X^2 - (\sum X)^2}\]\[\beta_0 = \bar{Y} - \beta_1 \bar{X}\]Cálculos:1. Calcule as somas:- \(\sum X = 2 + 4 + 6 + 8 + 10 = 30\)- \(\sum Y = 50 + 60 + 80 + 70 + 90 = 350\)- \(\sum XY = (2 \times 50) + (4 \times 60) + (6 \times 80) + (8 \times 70) + (10 \times 90) = 100 + 240 + 480 + 560 + 900 = 2280\)- \(\sum X^2 = 2^2 + 4^2 + 6^2 + 8^2 + 10^2 = 4 + 16 + 36 + 64 + 100 = 220\)2. Calcule \(\beta_1\):\[ \beta_1 = \frac{5 \times 2280 - 30 \times 350}{5 \times 220 - 30^2} = \frac{11400 - 10500}{1100 - 900} = \frac{900}{200} = 4.5 \]3. Calcule \(\beta_0\):\[ \bar{X} = \frac{30}{5} = 6, \quad \bar{Y} = \frac{350}{5} = 70 \]\[ \beta_0 = 70 - 4.5 \times 6 = 70 - 27 = 43 \]4. Equação da Regressão:\[ \hat{Y} = 43 + 4.5X \]Passo 2: Calcular os Valores Preditos Aplicamos a equação para cada \(X\):Aluno\(X\)\(Y\)\(\hat{Y} = 43 + 4.5X\)\(Y - \hat{Y}\) (Resíduo)1250\(43 + 4.5 \times 2 = 52\)\(50 - 52 = -2\)2460\(43 + 4.5 \times 4 = 61\)\(60 - 61 = -1\)3680\(43 + 4.5 \times 6 = 70\)\(80 - 70 = +10\)4870\(43 + 4.5 \times 8 = 79\)\(70 - 79 = -9\)51090\(43 + 4.5 \times 10 = 88\)\(90 - 88 = +2\)Passo 3: Calcular as Somas dos Quadrados1. Soma dos Quadrados Totais (\(SQ_{\text{Total}}\))Mede a variação total de \(Y\) em torno de sua média.\[ SQ_{\text{Total}} = \sum (Y_i - \bar{Y})^2 \]\(Y_i\)\(Y_i - \bar{Y}\)\((Y_i - \bar{Y})^2\)50-2040060-1010080+10100700090+20400\[ SQ_{\text{Total}} = 400 + 100 + 100 + 0 + 400 = 1000 \]2. Soma dos Quadrados da Regressão (\(SQ_{\text{Reg}}\))Mede quanto da variação de \(Y\) é explicada pelo modelo.\[ SQ_{\text{Reg}} = \sum (\hat{Y}_i - \bar{Y})^2 \]\(\hat{Y}_i\)\(\hat{Y}_i - \bar{Y}\)\((\hat{Y}_i - \bar{Y})^2\)52-1832461-981700079+98188+18324\[ SQ_{\text{Reg}} = 324 + 81 + 0 + 81 + 324 = 810 \]3. Soma dos Quadrados dos Resíduos (\(SQ_{\text{Res}}\) ou SSE)Mede o erro não explicado pelo modelo.\[ SSE = \sum (Y_i - \hat{Y}_i)^2 \]Resíduo (\(Y_i - \hat{Y}_i\))\((Y_i - \hat{Y}_i)^2\)-24-11+10100-981+24\[ SSE = 4 + 1 + 100 + 81 + 4 = 190 \](Observe que \(SQ_{\text{Total}} = SQ_{\text{Reg}} + SSE\): \(1000 = 810 + 190\))Passo 4: Calcular \(R^2\) (Coeficiente de Determinação)\[ R^2 = \frac{SQ_{\text{Reg}}}{SQ_{\text{Total}}} = \frac{810}{1000} = 0.81 \text{ ou } 81\% \]Interpretação:O modelo explica 81% da variação nas notas. Os 19% restantes são não explicados (erros/resíduos).Passo 5: Calcular SEE (Erro Padrão da Estimativa)\[SEE = \sqrt{\frac{SSE}{n - 2}} = \sqrt{\frac{190}{5 - 2}} = \sqrt{63.33} \approx 7.96\]Interpretação:O erro médio do modelo é de ±7.96 pontos na previsão das notas.Resumo dos Resultados- Equação da Regressão: \(\hat{Y} = 43 + 4.5X\)- R² = 0.81 (81% da variação explicada)- SSE = 190 (soma dos quadrados dos resíduos)- SEE ≈ 7.96 (erro médio das previsões)Exercícios1.Uma regressão entre idade (X) e pressão arterial (Y) tem \( R^2 = 0,64 \). O que isso significa?a) 64% da variação em Y é explicada por Xb) A correlação entre X e Y é 0,64c) O modelo é inválidod) 36% dos dados não são explicados por Y2. "Os resíduos formam um padrão em U". O que isso indica?a) Homocedasticidadeb) heterocedasticidadec) Normalidade perfeitad) Uma boa regressão3. Dada a tabela abaixo, calcule a regressão linear e interprete R² e SEE.X (Anos Exp.)Y (Salário)130.000340.000538.000755.0001. Calcular \( \beta_0 \) e \( \beta_1 \).2. Calcular \( R^2 \) e SEE.4. Faça uma regressão com os dados abaixo e discuta se o modelo é bom.X (Publicidade)Y (Vendas)100802007030090350110Dica: Calcule \( R^2 \), SEE e plote os resíduos!5. Calcule \( R^2 \), SEE e plote os resíduos da regressão abaixo. Podemos dizer que a regressão é boa? Verifique a Assimetria e Curtose.AlunoHoras (X)Nota (Y)Previsão (^Y)1250552460653680754870855109095Gabarito dos Exercícios1. a)2. b)
Faça login e participe da conversa
— Comentários 0
, Reações 1
Seja o primeiro a comentar