Material para acompanhar esta aulaBaixe a planilha encontrada aqui no Google Planilhas. Usaremos esta planilha para a aula. Baixe ela para CSV, o método mais comum de guardar um banco de dados que pode ser lido por qualquer linguagem (Comma-Separated Values).Crie um ambiente de desenvolvimento python3 ou utilize ambientes online já prontos como o jupyter lab online e importe o banco de dados.Scipy em PythonComece baixando os dados para CSV, renomeando-os para "dados-3.csv" para ficar mais fácil de mexer. Vamos usar os pacotes pandas, numpy, statsmodels, scipy e matplotlib no python. Abaixo pode ver como importar cada um:Importação dos pacotes em pythonTempo como índiceRepare que estamos usando decimal="," e thousands="." justamente por nossos dados estarem em português. Agora vamos usar o tempo como índice da nossa tabela de dados. Abaixo está o código para deixar o tempo como índice.Transformação da coluna Tempo em índiceApós transformar a coluna Tempo em índice, vamos verificar o quanto o preço do Ouro aumentou no tempo. Repare que estou usando ouro aqui, mas recomendo vocês testarem outros preços de ações. Para saber como cresceu no tempo usamos as funções .diff() ou pct_change().Histograma da variação do preço do OuroVamos verificar como aparenta nossos dados. Para isso, a melhor forma é realizar um gráfico de histograma como abaixo.Criando o histograma do preço do ouroO resultado ficou:Histograma da variaçãoRepare que este histograma lembra a distribuição normal!Teste de normalidadeComo nossos dados lembram muito uma distribuição normal, podemos fazer um teste de normalidade para verificar a hipótese que de fato é uma distribuição normal. Para isso usamos o scipy com a função normaltest.Teste de normalidade com ScipyO resultado deu uma probabilidade muito pequena! Uma probabilidade de 4.0693e-07. Pode ser uma coincidência? Claro que pode, mas a chance é tão pequena que podemos rejeitar a hipótese nula que não há normalidade. 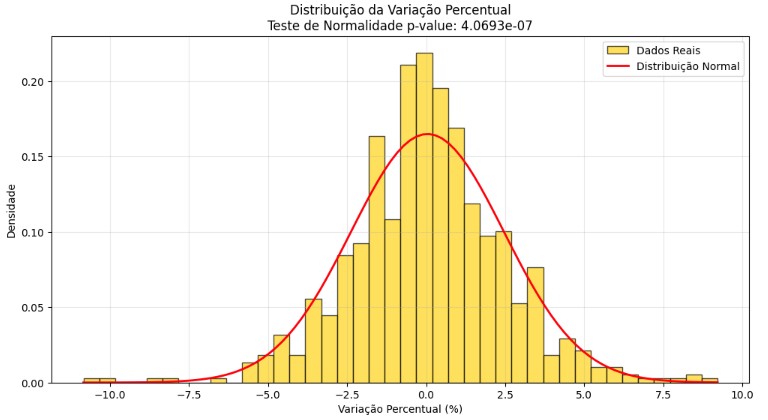Veja abaixo o gráfico da normal plotado com nossos dados:Distribuição real vs Distribuição normalIdentificando OutliersVamos considerar de agora em diante então que a variação diária dos preços do Ouro seguem uma distribuição Normal. Como isso podemos verificar dias com anomalia. Esses dias com anomalia são chamados de "outliers", dias muito pouco prováveis. Para isso vamos utilizar a distância de 3 desvios padrões para caracterizar que um dado está muito longe da média e é de fato uma anomalia. Essa característica de 3 desvios padrões é muito usada na indústria, mas vocês podem modificar o valor para caso queiram detectar anomalias ainda maiores.Código para detectar OutliersOs dias detectados como outliers para o Ouro foram:DiaVariação %2014-11-069.2123062014-11-28-8.1771722014-12-177.5590812015-10-027.8665082016-02-088.7100892016-05-04-10.8404772016-06-038.4374262016-10-04-8.7556682016-11-10-10.078868Se quiser pode procurar no jornal cada dia desses. Será que aconteceu algo diferente nesses dias?Devemos investir em Ouro?Agora que sabemos que a distribuição é Normal, temos dados o suficiente para dizer que Ouro está crescendo no tempo? 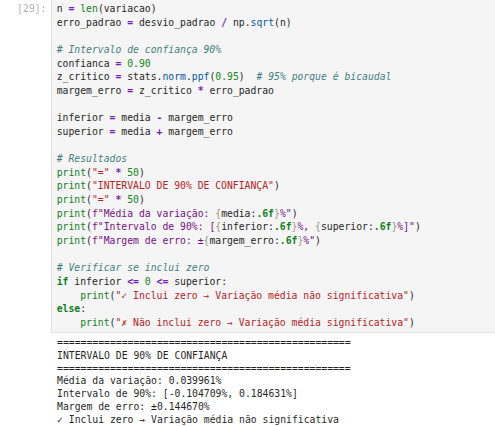Para isso precisamos construir um intervalo de confiança do aumento do Ouro usando nossa amostra.Construção do Intervalo de confiança com ScipyRepare que apesar do Ouro ter uma média amostral positiva, ainda não temos dado o suficiente para confirmar que a variação do Ouro é acima de zero.E se quisermos ter mais certeza, quantas amostras precisamos?Imagine então que queremos verificar se de fato o Ouro é um investimento seguro. Será que só 3 anos de dados é o suficiente? Quantos dias precisamos para nossa amostra? 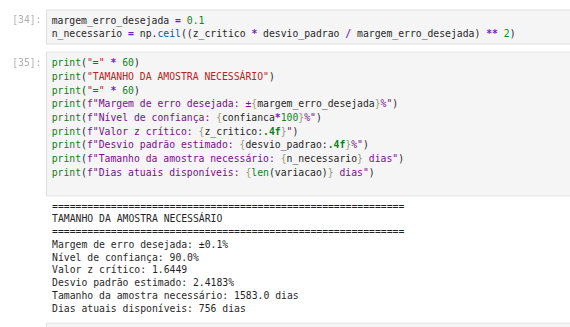Vamos ver abaixo como faríamos para ter uma margem de erro de apenas 0,1% no aumento, podendo nos ajudar com a inferência sobre esse investimento.Tamanho Amostral com ScipyQual deverá ser o tema da prova?
Faça login e participe da conversa
— Comentários 0
, Reações 1
Seja o primeiro a comentar