Como fazer Regressão com Statsmodels no Python

11/06/25 •0•0

Descubra como realizar análises de regressão com Statsmodels em Python. Da preparação de dados ao ajuste do modelo, aprenda instruções passo a passo para aproveitar esta poderosa ferramenta estatística para uma modelagem preditiva robusta.

Escrito porLeon

Material para acompanhar esta aula

Baixe a planilha encontrada aqui no Google Planilhas. Usaremos esta planilha para a aula. Baixe ela para CSV, o método mais comum de guardar um banco de dados que pode ser lido por qualquer linguagem (Comma-Separated Values).

Crie um ambiente de desenvolvimento python3 ou utilize ambientes online já prontos como o jupyter lab online e importe o banco de dados.

Statsmodels em Python

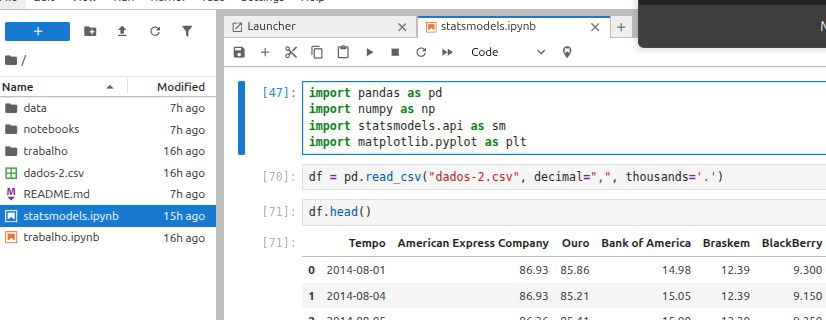
Comece baixando os dados para CSV, renomeando-os para "dados-2.csv" para ficar mais fácil de mexer. Vamos usar os pacotes pandas, numpy, statsmodels e matplotlib no python. Abaixo pode ver como importar cada um:

Importação dos pacotes em python

Tempo como índice

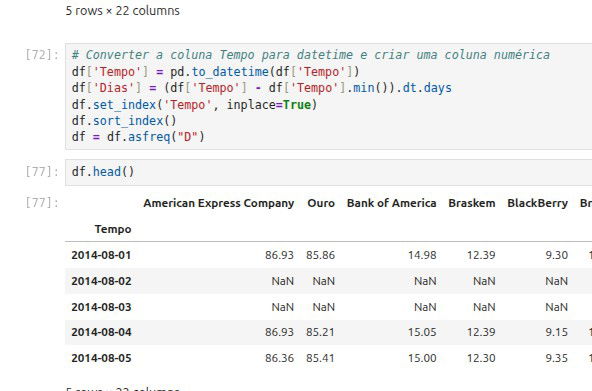
Repare que estamos usando decimal="," e thousands="." justamente por nossos dados estarem em português. Agora vamos usar o tempo como índice da nossa tabela de dados. Abaixo está o código para deixar o tempo como índice e também criar uma coluna "Dias". A coluna "Dias" será usada na regressão linear, com ela vamos verificar quando cada ação está crescendo no tempo usando o coeficiente angular.

Transformação para usar o tempo como índice

Matriz de correlação

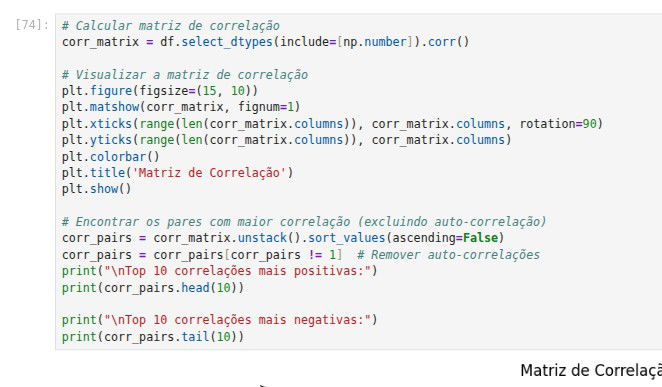
Antes de começar as regressões, vamos para uma análise muito importante para quem investe: a matriz de correlação. Essa matriz mostra como cada ação é correlacionada. Caso você queira fazer uma carteira de investimentos no futuro, lembre-se de escolher ações correlacionadas negativamente entre elas, assim diminui o risco da carteira. Abaixo está o código para calcular a matriz de correlação:

Cálculo das correlações

A matriz deve ficar assim ao final:

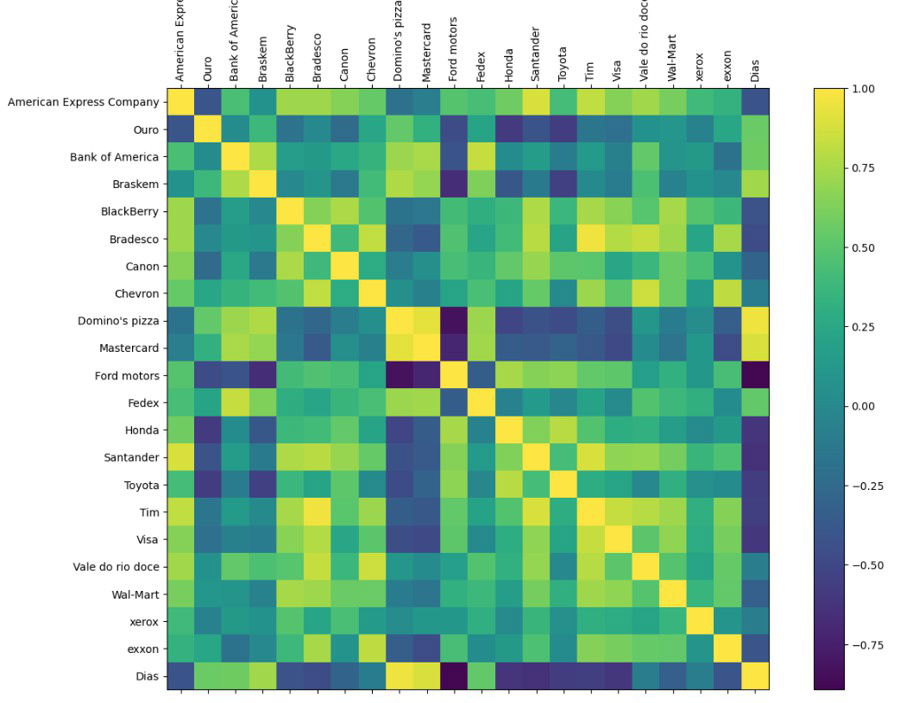
Matriz de correlação entre as ações

Abaixo está o que foi printado pelo python com relação as correlações. Correlações mais positivas:

Empresa 1	Empresa 2	Correlação
Bradesco	Tim	0.957497
Tim	Bradesco	0.957497
Domino's pizza	Dias	0.948813
Dias	Domino's pizza	0.948813
Mastercard	Domino's pizza	0.921368
Domino's pizza	Mastercard	0.921368
Santander	American Express Company	0.888684
American Express Company	Santander	0.888684
Tim	Santander	0.888301
Santander	Tim	0.888301

Correlações mais negativas:

Empresa 1	Empresa 2	Correlação
Dias	Santander	-0.642465
Santander	Dias	-0.642465
Ford motors	Braskem	-0.668737
Braskem	Ford motors	-0.668737
Ford motors	Mastercard	-0.708027
Mastercard	Ford motors	-0.708027
Domino's pizza	Ford motors	-0.826345
Ford motors	Domino's pizza	-0.826345

Regressão linear Simples

Vamos agora de fato utilizar o Statsmodels. Abaixo está o código para fazer uma regressão linear simples entre Ouro e número de Dias.

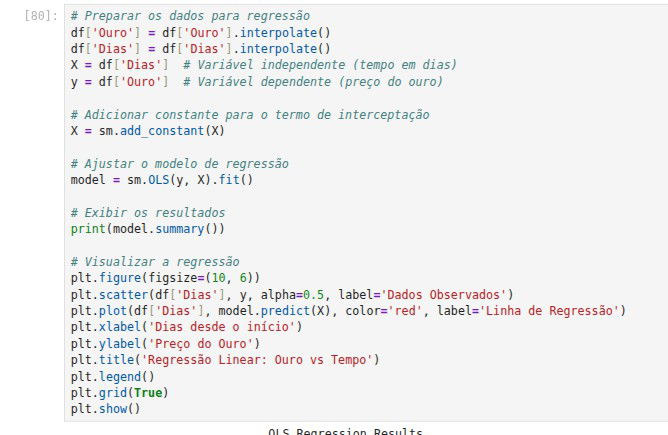
Regressão linear no Statsmodels

A regressão linear traz diversos resultados, veja a tabela abaixo e tente interpretar cada parâmetro:

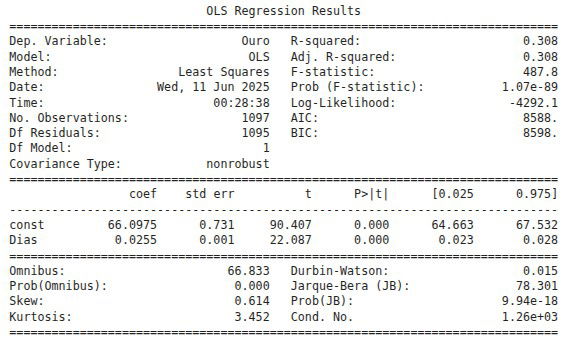
OLS resultados

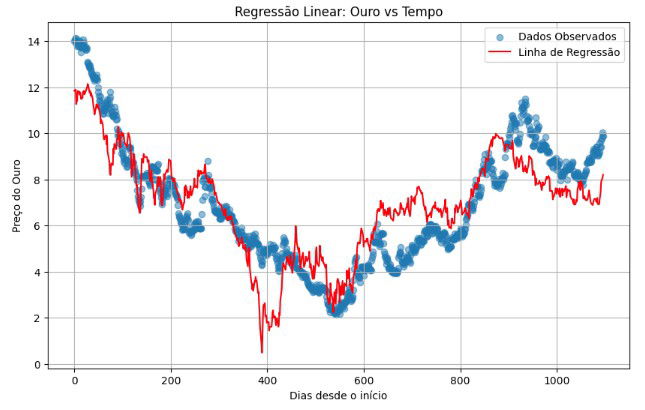
Abaixo está nossa previsão e os pontos observados da realidade:

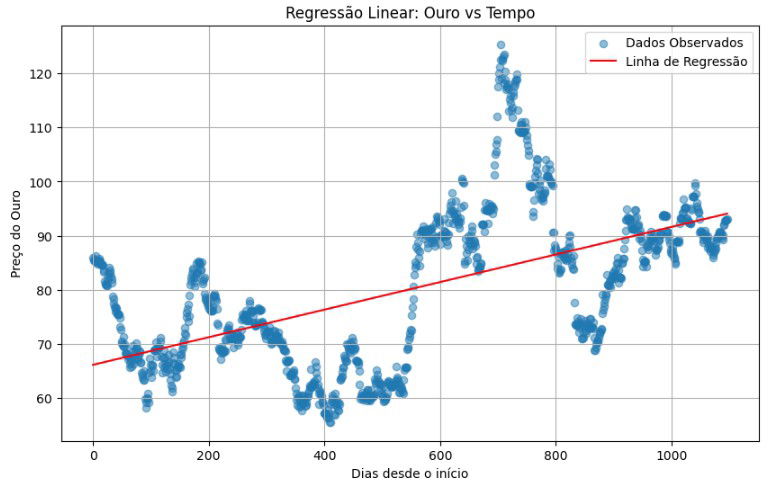
Previsão vs observado

Não é das melhores regressões né? Vamos olhar para os resíduos também.

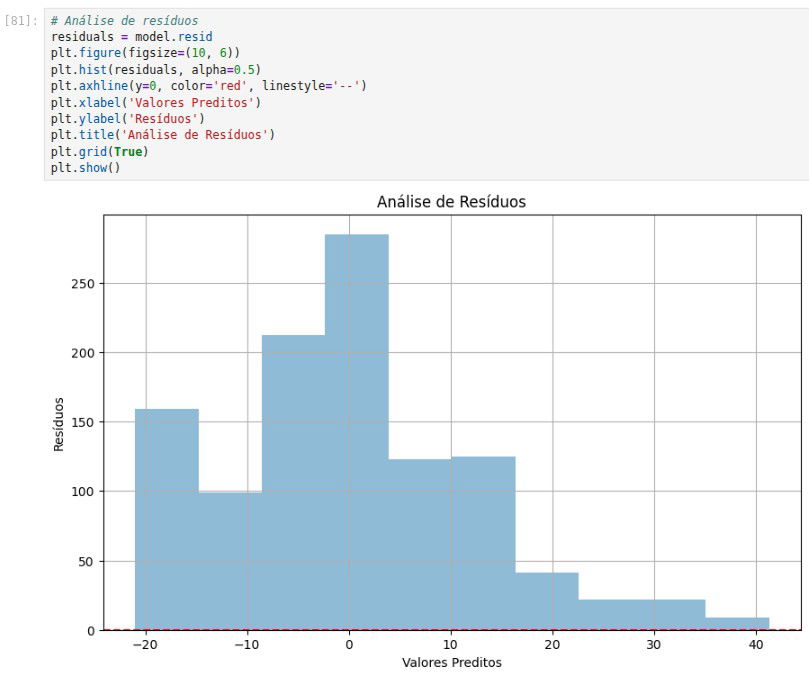
Os resíduos se mostram com uma tendência e não simétricos

Regressão ARIMA

Se nosso amigo Regressão Linear não consegue prever, podemos procurar outros modelos. Vamos então tentar fazer uma regressão ARIMA(1,1,1) entre o valor do Ouro e o Tempo.

Código python para ARIMA

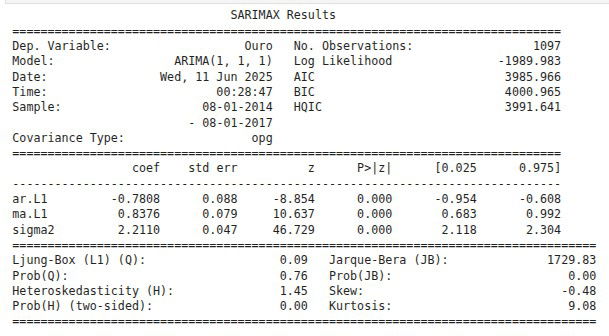
Resultado da ARIMA

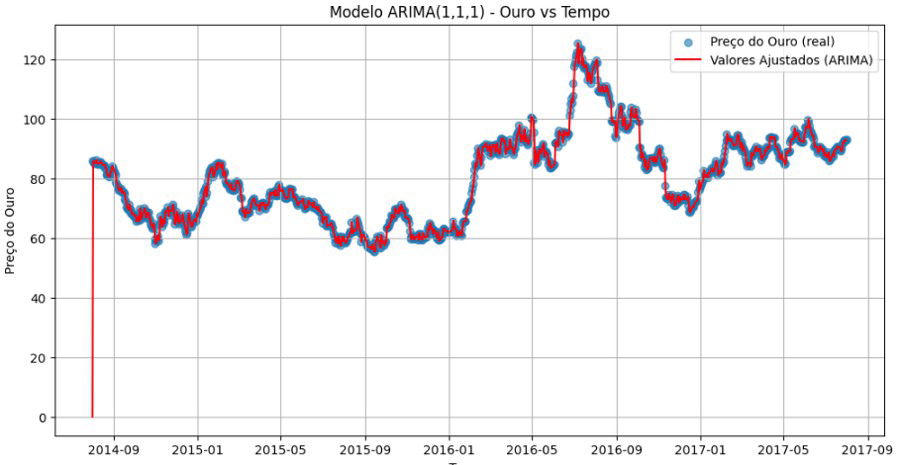
Previsto vs Observado com ARIMA

Por mais que a previsão parece boa, não podemos nos esquecer de olhar para os resíduos:

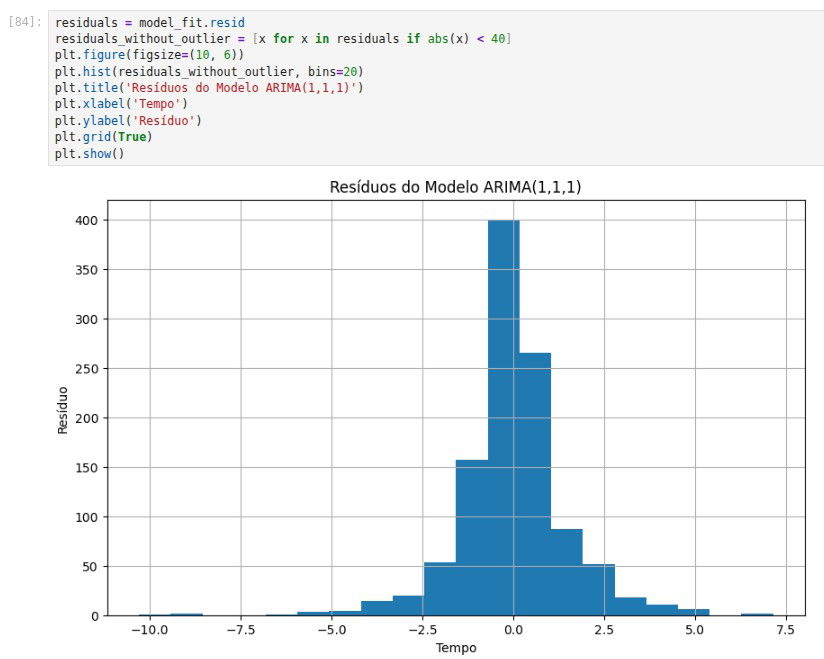
Resíduos da ARIMA

Conjunto treino vs conjunto teste

Por mais que a ARIMA tenha tido um ótimo resultado, é bom verificarmos dividindo nossa amostra em dois conjuntos ao menos: conjunto treino e conjunto teste. Vamos dividir pela metade, treinar nosso modelo com o conjunto treino e verificar se no teste ele também possui bons resultados.

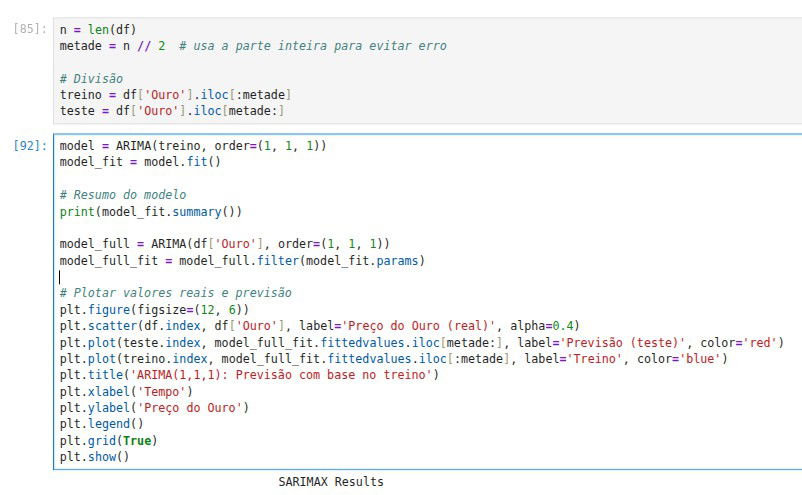
Criando o conjunto teste e treino e fazendo nova regressão

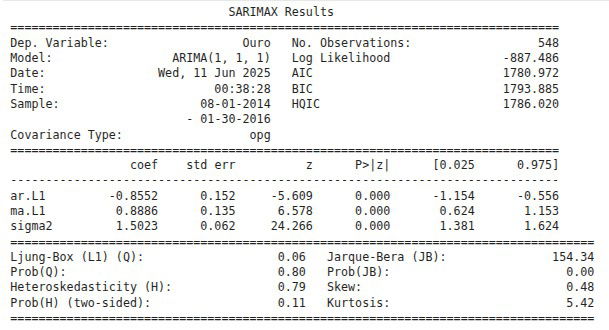
Resultados da ARIMA de treino

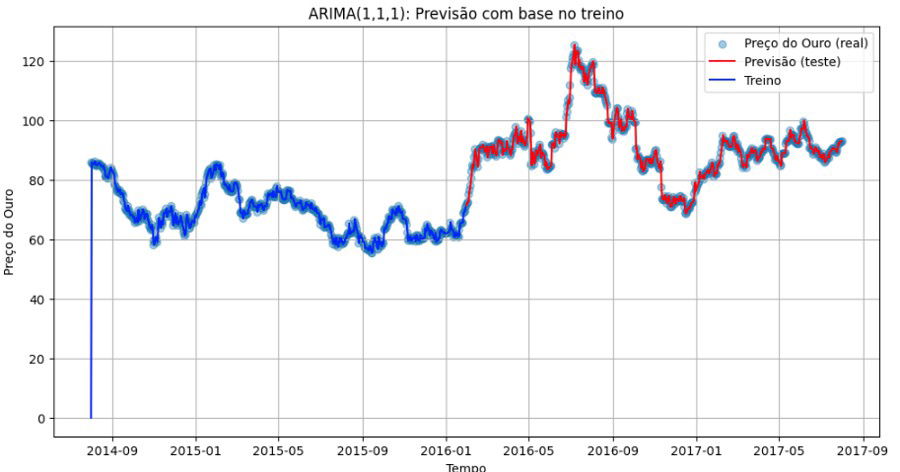
Previsão final:

Teste, Treino e valores observados

Regressão Multivariada

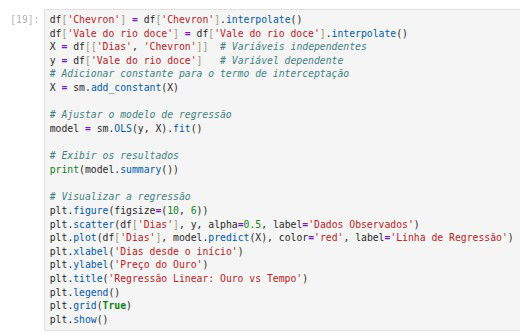
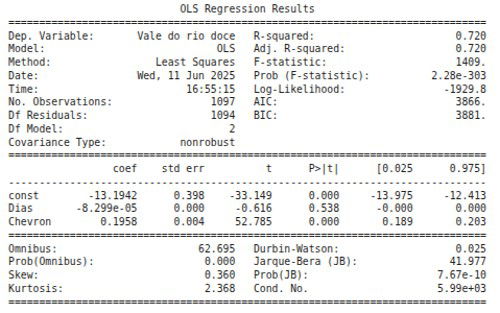
Caso você não queira trabalhar com ARIMA, é possível fazer uma regressão Multivariada escolhendo ações correlacionadas com a sua para fazer previsões. No exemplo abaixo eu uso o preço da Chevron e o número de Dias para prever o preço da Vale do Rio Doce.