Estatística em Python: Usando Pandas para compreensão de sua distribuição

14/05/25, editado 15/05/25 •0•0

Descubra como analisar dados estatísticos em Python usando a poderosa biblioteca Pandas. Aprenda a interpretar e visualizar a distribuição dos seus dados para obter melhores insights e facilitar a tomada de decisões.

Escrito porLeon

Material para acompanhar esta aula

Baixe a planilha encontrada aqui no Google Planilhas. Usaremos esta planilha para a aula. Baixe ela para CSV, o método mais comum de guardar um banco de dados que pode ser lido por qualquer linguagem (Comma-Separated Values).

Crie um ambiente de desenvolvimento python3 ou utilize ambientes online já prontos como o jupyter lab online e importe o banco de dados.

Pandas em Python

Ficará assim sua pasta caso utilize a versão online:

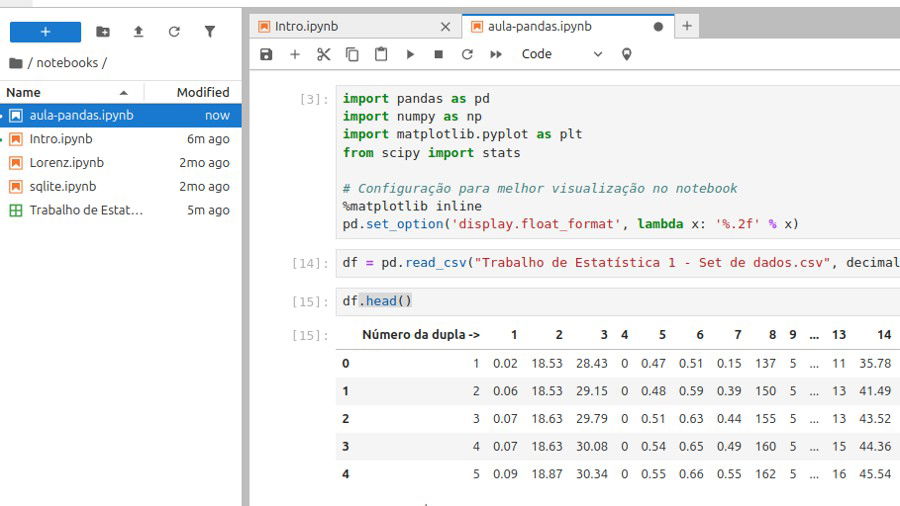
Pasta no jupyter lab online

Como pode observar, vamos usar pandas para compreender nosso banco de dados. Para importar pandas use:

import pandas as pd

E vamos abrir nosso banco de dados usando read_csv:

df = pd.read_csv("Trabalho de Estatística 1 - Set de dados.csv", decimal=',')

Lembre de utilizar decimal="," ou ele não compreenderá os números separados por vírgulas como números já que python geralmente assume que escrevemos que nem pessoas dos Estados Unidos e não do Brasil.

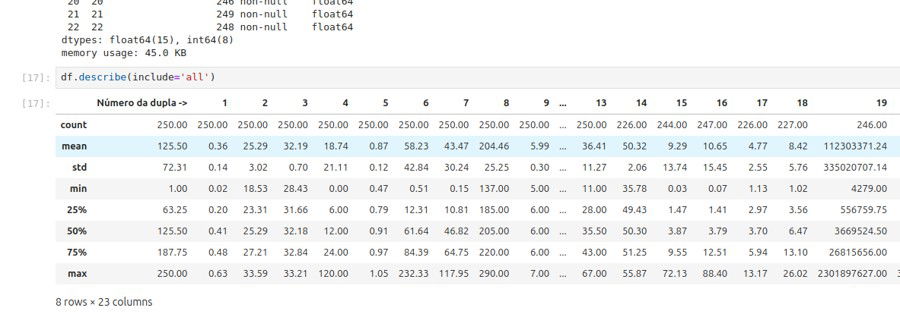
Use agora .info() ou .describe() no banco para ele nos fornecer dados rápidos sobre sua distribuição:

Exemplo com .describe()

Para calcular a média, moda e mediana use respectivamente .mean() .mode() e .median():

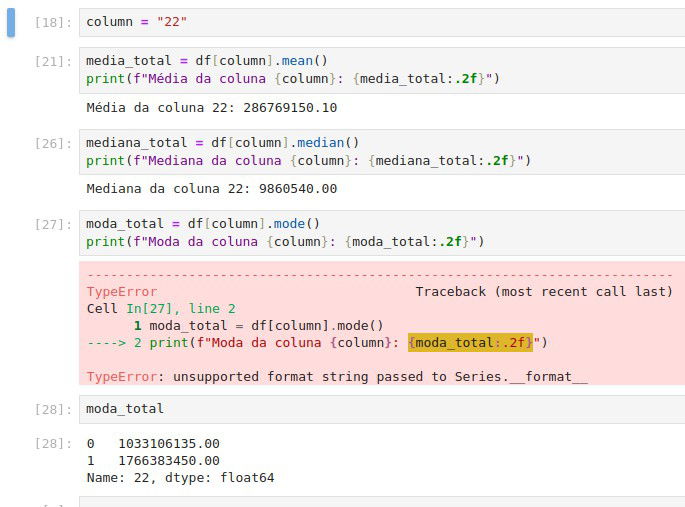
Cálculo da média, moda e mediana em pandas

Perceba que ele te comunica caso tenha mais de 1 moda.

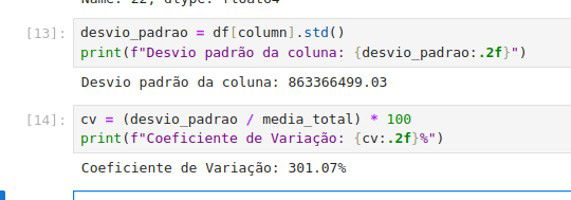
Desvio padrão e Coeficiente de Variação (CV) podem ser calculados das seguintes maneiras:

Desvio padrão e CV no pandas

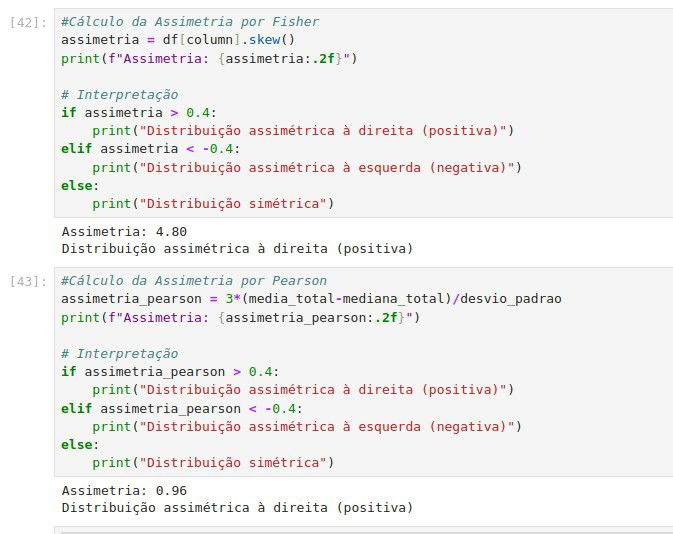
Agora vamos para o cálculo da Assimetria:

Assimetria em Pandas

A fórmula utilizada pelo Pandas para cálculo da assimetria (skewness) é:

\[ G_1 = \frac{n}{(n-1)(n-2)} \sum_{i=1}^n \left( \frac{x_i - \bar{x}}{s} \right)^3 \]

Onde:

- \( n \) = número de observações

- \( x_i \) = cada valor individual

- \( \bar{x} \) = média amostral

- \( s \) = desvio padrão amostral (com \( n-1 \) graus de liberdade)

A função `.skew()` foi implementada seguindo a abordagem de Fisher e é uma fórmula diferente de calcular assimetria comparada a Pearson, com:

- Correção para viés em pequenas amostras

- Consistência com outras implementações populares

- Tratamento adequado de valores ausentes (NaN)

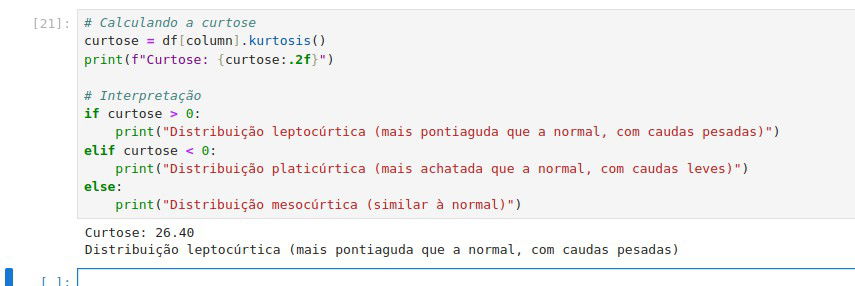
Agora o cálculo de curtose:

Curtose em pandas

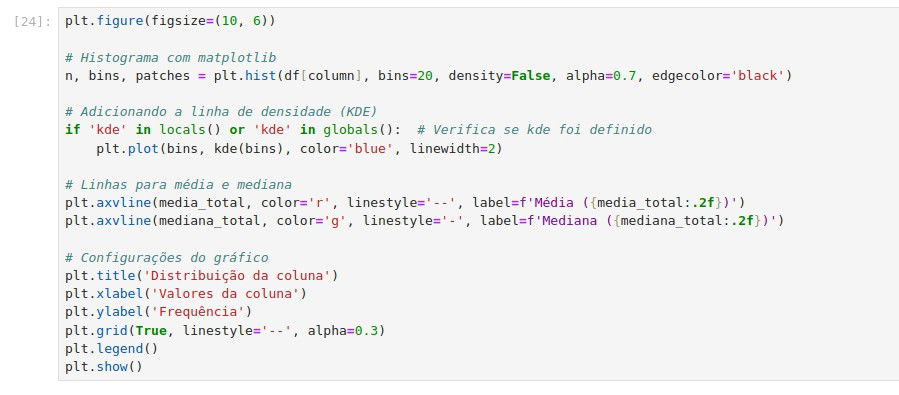
Agora vamos fazer a curva usando histograma:

Use matplotlib para criar o histograma em python

O gráfico final:

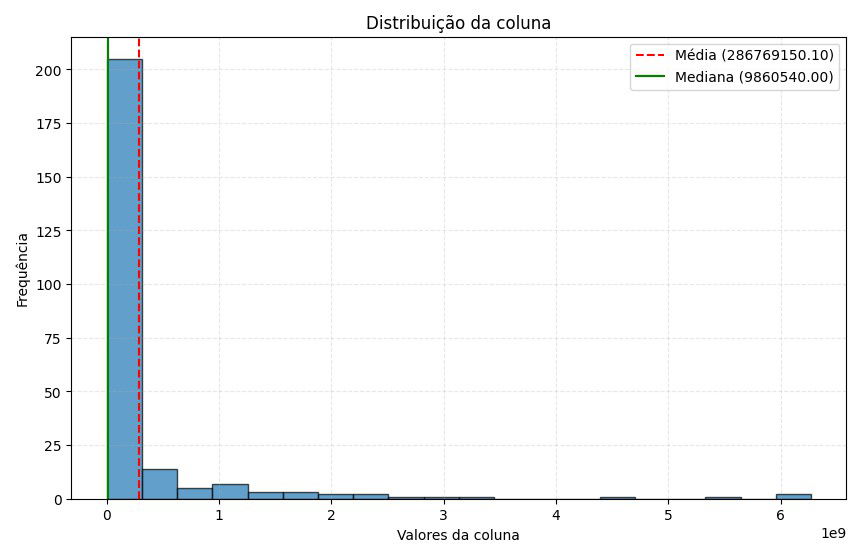
Gráfico construído pelo matplotlib

Qual curva consegue enxergar? Aqui vejo um Jota.

Você também pode fazer um boxplot para ver seus dados:

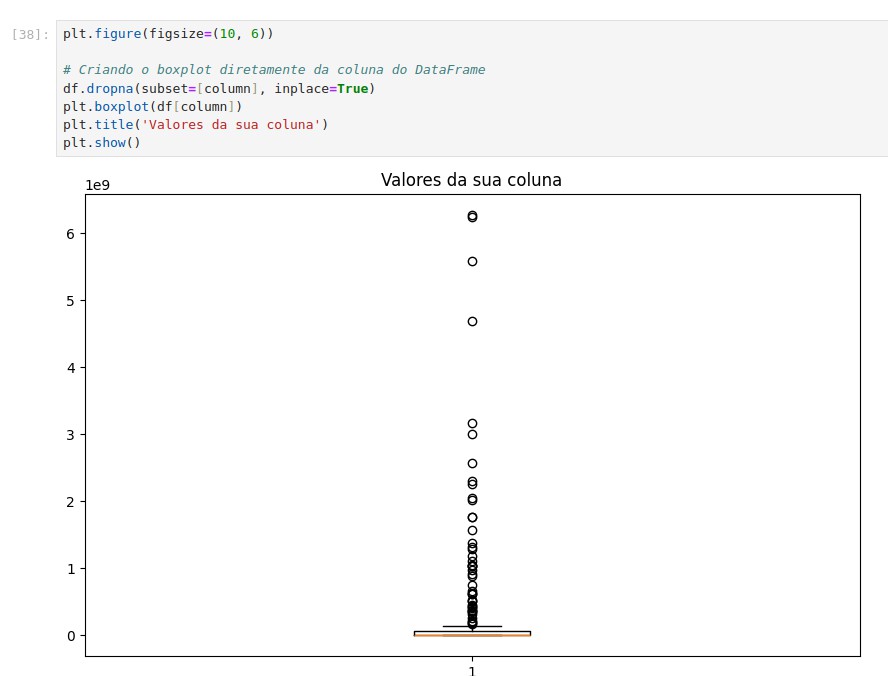
Boxplot no matplotlib

Apesar que boxplot não é o mais recomendado com curvas de jota.

Transformando seus dados

Como a curva parece de Jota podemos fazer transformações para que a curva se torna de sino, uma curva mais fácil de trabalhar. Nesse meu caso vou transformar usando o logaritmo:

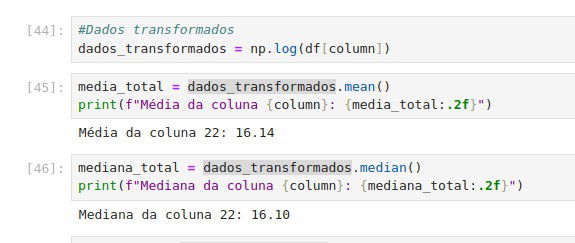
Transformação para logarítimo em pandas

Repare que a transformação pode ser feita de diversas maneiras: podemos tirar o logaritmo, podemos fazer a raiz quadrada. Neste caso achei apropriado o logaritmo por ter uma cauda à direita muita acentuada e sem zeros. Geralmente transformamos em logaritmo valores financeiros (salários, preços de ações), tamanhos populacionais, tempos de resposta em sistemas e dados de vendas com outliers positivos. E geralmente transformamos usando raiz quadrado quando há: número de visitas a websites, contagem de acidentes, número de produtos vendidos e dados de frequência de eventos.

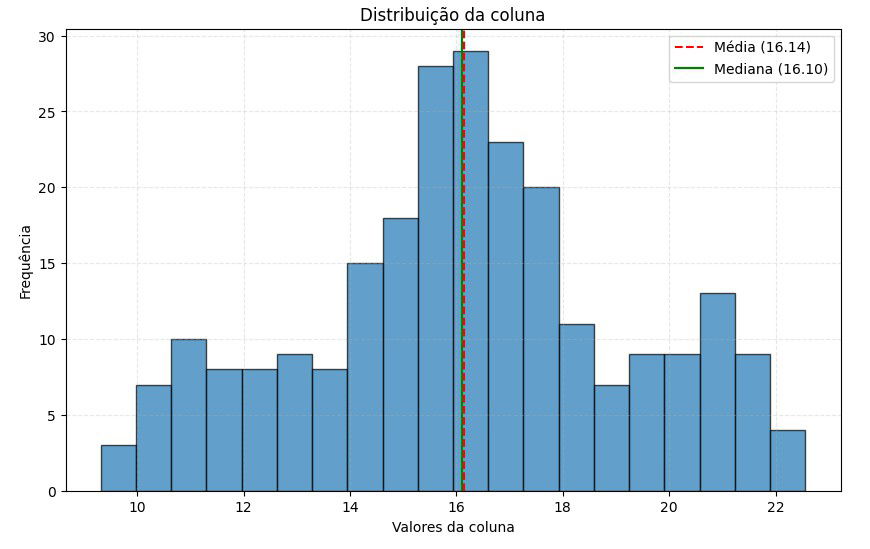
Histograma da distribuição log transformada

Olhando o histograma parece que acertamos na transformação!

Boxplot da Log Transformada

Se analisarmos a média, desvio-padrão, assimetria e curtose podemos ter mais certeza que fizemos bem em transformar!

Trabalho: faça você mesmo!

Escolha um número para trabalhar dentro do banco de dados proporcionado e responda as seguintes perguntas:

1) Qual a média da distribuição?

2) Qual a mediana da distribuição?

3) A distribuição possui moda?

4) Qual o desvio padrão da distribuição?

5) Qual o coeficiente de variação do seu conjunto de dados?

6) Faça o gráfico de distribuição de frequências

7) Qual a forma da curva? (curva em forma de sino, curva em forma de jota, curva em forma de u, curva em forma uniforme, bimodal, trimodal, multimodal……)

8) Analisando os valores das variáveis, quais possíveis dados elas podem representar?

9) Faça o Boxplot da sua distribuição