Distribuição de Poisson
A Distribuição de Poisson é usada para modelar o número de eventos que ocorrem em um intervalo de tempo ou espaço, quando esses eventos acontecem com uma taxa média conhecida e são independentes do tempo desde o último evento. É ideal para situações em que eventos raros ocorrem de forma aleatória.
Fórmula da Distribuição de Poisson
A probabilidade de ocorrerem exatamente \( k \) eventos em um intervalo é dada por:
\[ P(X = k) = \frac{e^{-\lambda} \cdot \lambda^k}{k!} \]
Onde:
- \( \lambda \): Taxa média de ocorrências no intervalo.
- \( k \): Número de eventos desejados.
- \( e \): Número de Euler (aproximadamente 2,71828).
- \( k! \): Fatorial de \( k \).
Exemplos da Vida Real
Exemplo 1: Chamadas telefônicas
- Situação: Um call center recebe, em média, 5 chamadas por hora.
- Pergunta: Qual a probabilidade de receber exatamente 3 chamadas em uma hora?
Resolução:\[ \lambda = 5, \quad k = 3 \]
\[ P(X = 3) = \frac{e^{-5} \cdot 5^3}{3!} = \frac{0,0067 \cdot 125}{6} \approx 0,1404 \quad (14,04\%) \]
Exemplo 2: Acidentes em uma rodovia
- Situação: Em uma rodovia, ocorrem, em média, 2 acidentes por dia.
- Pergunta: Qual a probabilidade de ocorrerem exatamente 4 acidentes em um dia?
Resolução:\[ \lambda = 2, \quad k = 4 \]
\[ P(X = 4) = \frac{e^{-2} \cdot 2^4}{4!} = \frac{0,1353 \cdot 16}{24} \approx 0,0902 \quad (9,02\%) \]
Exemplo 3: Defeitos em uma linha de produção
- Situação: Uma fábrica produz, em média, 1 peça defeituosa a cada 10 horas.
- Pergunta: Qual a probabilidade de encontrar exatamente 2 peças defeituosas em 20 horas?
Resolução:\[ \lambda = 2 \quad (\text{20 horas} \div \text{10 horas por defeito}) \]
\[ P(X = 2) = \frac{e^{-2} \cdot 2^2}{2!} = \frac{0,1353 \cdot 4}{2} \approx 0,2707 \quad (27,07\%) \]
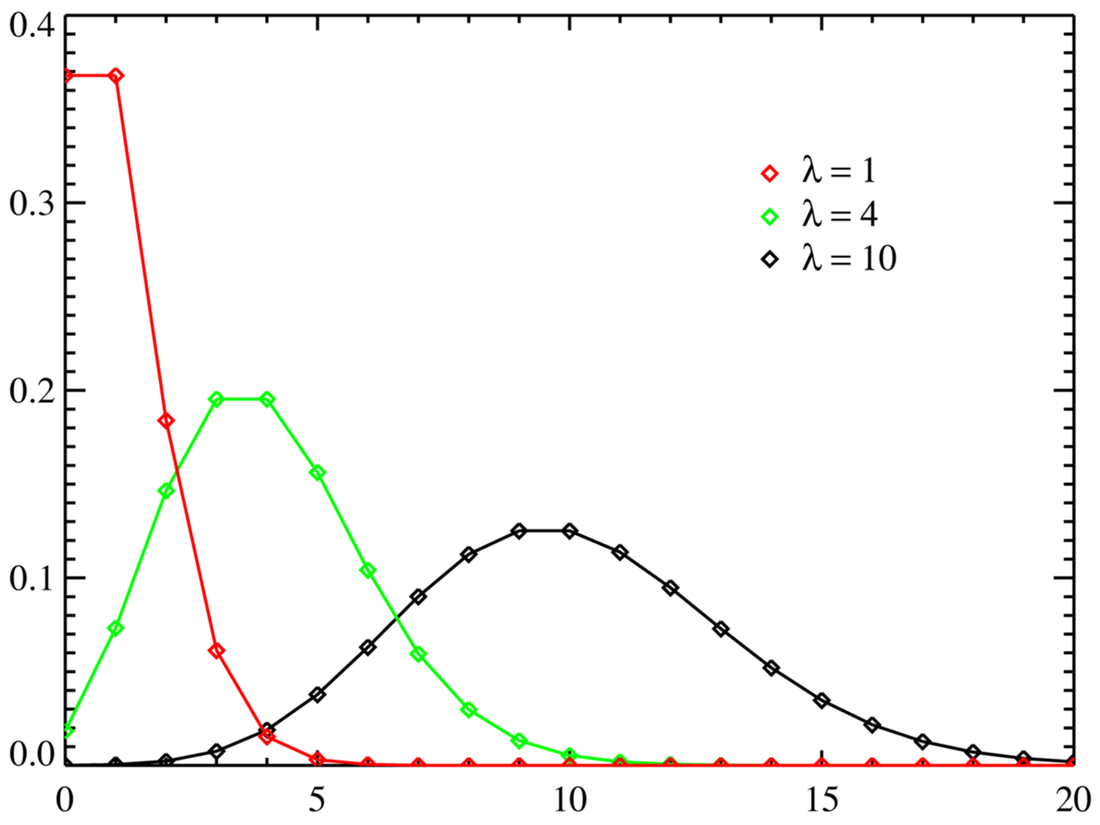
Contexto da Poisson
A função de Poisson (ou distribuição de Poisson) surgiu no contexto da teoria das probabilidades no início do século XIX, desenvolvida pelo matemático francês Siméon Denis Poisson (1781–1840). Ela foi introduzida em seu trabalho "Recherches sur la probabilité des jugements en matière criminelle et en matière civile" (1837), onde Poisson estudava a probabilidade de eventos raros em grandes populações, como condenações criminais.
A distribuição de Poisson surgiu como uma aproximação da distribuição binomial quando o número de tentativas (\( n \)) é grande e a probabilidade de sucesso (\( p \)) é pequena, mantendo o produto \( \lambda = n \cdot p \) constante. Ou seja, ela modela a ocorrência de eventos raros em um intervalo fixo de tempo ou espaço.
Quando usar Poisson e quando usar Binomial?
A escolha entre usar a Distribuição Binomial e a Distribuição de Poisson depende das características do problema que você está analisando. Ambas são usadas para modelar o número de eventos, mas em contextos diferentes.
Quando usar Distribuição Binomial
A Distribuição Binomial é usada quando:
1. Número fixo de tentativas (\( n \)): O experimento consiste em um número fixo e conhecido de tentativas.
2. Dois resultados possíveis: Cada tentativa tem apenas dois resultados possíveis: sucesso ou fracasso.
3. Probabilidade constante (\( p \)): A probabilidade de sucesso (\( p \)) é a mesma em cada tentativa.
4. Tentativas independentes: O resultado de uma tentativa não afeta o resultado das outras.
Exemplos de aplicação:
- Jogar uma moeda \( n \) vezes e contar o número de caras.
- Testar \( n \) produtos e contar quantos estão defeituosos.
- Realizar \( n \) tentativas de chute a gol e contar quantos gols são marcados.
Quando usar Distribuição de Poisson
A Distribuição de Poisson é usada quando:
1. Eventos raros: O evento de interesse é raro em relação ao intervalo de tempo ou espaço.
2. Taxa média conhecida (\( \lambda \)): O número médio de ocorrências (\( \lambda \)) em um intervalo é conhecido.
3. Eventos independentes: A ocorrência de um evento não afeta a ocorrência de outros.
4. Intervalo contínuo: Os eventos podem ocorrer em qualquer ponto de um intervalo contínuo (tempo, espaço, etc.).
Exemplos de aplicação:
- Número de chamadas recebidas em um call center por hora.
- Número de acidentes em uma rodovia por dia.
- Número de erros de digitação em uma página de texto.
- Número de clientes que chegam a um restaurante por minuto.
Exercícios
1. Chamadas telefônicas:
- Um call center recebe, em média, 4 chamadas por hora. Qual a probabilidade de receber exatamente 6 chamadas em uma hora?
2. Acidentes em uma rodovia:
- Em uma rodovia, ocorrem, em média, 3 acidentes por dia. Qual a probabilidade de ocorrerem exatamente 5 acidentes em um dia?
3. Defeitos em uma linha de produção:
- Uma fábrica produz, em média, 2 peças defeituosas a cada 8 horas. Qual a probabilidade de encontrar exatamente 3 peças defeituosas em 24 horas?
4. Chegadas de clientes:
- Um restaurante recebe, em média, 10 clientes por hora. Qual a probabilidade de receber exatamente 12 clientes em uma hora?
5. E-mails recebidos:
- Um funcionário recebe, em média, 8 e-mails por hora. Qual a probabilidade de receber exatamente 10 e-mails em uma hora?
6. Falhas em um sistema:
- Um sistema falha, em média, 1 vez por dia. Qual a probabilidade de o sistema falhar exatamente 2 vezes em um dia?
7. Nascimentos em um hospital:
- Um hospital registra, em média, 5 nascimentos por dia. Qual a probabilidade de ocorrerem exatamente 7 nascimentos em um dia?
8. Carros passando por um pedágio:
- Um pedágio registra, em média, 20 carros por minuto. Qual a probabilidade de passarem exatamente 25 carros em um minuto?
9. Erros de digitação:
- Um digitador comete, em média, 3 erros por página. Qual a probabilidade de cometer exatamente 5 erros em uma página?
10. Chuva em uma cidade:
- Em uma cidade, chove, em média, 4 dias por mês. Qual a probabilidade de chover exatamente 6 dias em um mês?
Gabarito
1. 10,42%
2. 10,08%
3. 8,92%
4. 9,48%
5. 9,93%
6. 18,39%
7. 10,44%
8. 4,46%
9. 10,08%
10. 10,42%












— Comentários 0
, Reações 1
Seja o primeiro a comentar