Medidas de posição
O estudo realizado até o momento permite-nos descrever, de modo geral, os grupos dos valores que uma variável pode assumir. Dessa forma, sabe-se onde se concentram os valores e como a frequência se comporta.
Porém, para ressaltar as tendências características de cada distribuição, isoladamente, ou em confronto com outras, necessitamos conceitos que se expressem através de números, que nos permita traduzir essa tendência.
Esses conceitos são denominados elementos típicos da distribuição:
- Medidas de posição;
- Medidas de dispersão;
- Medidas de assimetria;
- Medidas de curtose;
Dentre os elementos típicos, para esta aula se destacará as medidas de posição, orientando quanto à posição da distribuição em relação ao eixo horizontal (eixo das abscissas).
Essas medidas englobam:
- Média aritmética;
- Mediana;
- Moda.
Outras medidas de posição podem ser as separatrizes:
- A própria mediana;
- Quartis;
- Percentis.
Média aritmética
Média com dados não-agrupados
A média aritmética simples é o quociente da divisão entre a soma dos valores da variável pelo número delas:
\[ \bar{x} = \frac{\sum{x_i}}{n} \]
As vezes a média pode ser um número diferente de todos os da série de dados que ela representa. Um exemplo:
Sabendo que a produção leiteira da vaca A, durante uma semana, foi de 10, 12, 13, 13, 15, 16, 19. Qual foi a produção média da semana?
\[ \bar{x} = \frac{10 + 13 + 13 + 15 + 16 + 19 + 12}{7} = 14 \]
14 neste caso é o número representativo dessa série de dados, embora não esteja nos dados originais. Neste caso, costumamos dizer que a média não tem existência concreta.
Há de perceber que a média nos dá uma posição desse conjunto de dados, como a média é 14, imagina-se que a vaca não dará mais de 100 litros de leite em um dia ou número de leite negativo.
Desvio em relação à média
> Denominamos desvio em relação à média a diferença entre cada elemento de um conjunto de valores e a média aritmética.
Para cada valor no conjunto de dados temos:
\[ d_i = x_i - \bar{x_i} \]
Para o exemplo anterior:
\[ d_1 = x_1 - \bar{x_1} = 10 - 14 = -4 \]
\[ d_2 = 12 - 14 = -2 \]
\[ d_3 = 13 - 14 = -1 \]
\[ d_4 = 13 - 14 = -1 \]
\[ d_5 = 15 - 14 = 1 \]
\[ d_6 = 16 - 14 = 2 \]
\[ d_7 = 19 - 14 = 5 \]
Propriedades da média
1º - A soma algébrica dos desvio é nula.
No exemplo:
\[ d_1 + d_2 + d_3 + d_4 + d_5 + d_6 + d_7 = -4 -2-1-1+1+2+5 = 0 \]
2º - Somando-se (ou subtraindo-se) uma constante c de todos os valores de uma variável, a média do conjunto fica aumentada (ou diminuída) dessa constante.
Para cada x:
\[ \bar{x} + c = \frac{\sum{x_i + c}}{n} \]
No exemplo da vaca, vamos somar 5 para cada valor obtendo: 15, 17, 18, 18, 20, 21, 24. Logo, a média:
\[ \bar{x} = \frac{15 + 17 + 18 + 18 +20+ 21+ 24}{7} = 19 \]
3º - Multiplicando-se (ou dividindo-se) todos os valores de uma variável por uma constante c, a média do conjunto fica multiplicada (ou dividida) por essa constante.
\[ \bar{x} · c = \frac{\sum{x_i · c}}{n} \]
No exemplo da vaca, vamos multiplicar por 2 cada valor obtendo: 20, 24, 26, 26, 30, 32, 38. Logo, a média:
\[ \bar{x} = \frac{20+ 24+ 26+ 26+ 30+ 32+ 38}{7} = 28 \]
Média com dados agrupados: sem intervalo de classe
A tabela abaixo representa a distribuição relativa a 34 famílias de 4 filhos, tomando como variável o número de filhos do sexo masculino:
| Nº de meninos | Frequência |
|---|---|
| 0 | 2 |
| 1 | 6 |
| 2 | 10 |
| 3 | 12 |
| 4 | 4 |
Considerando a distribuição de frequência acima, percebe-se que a frequência são o número de vezes que se repete cada dado, logo ela funciona como fator de ponderação, o que nos leva a calcular a média aritmética ponderada. Sua fórmula é a seguinte:
\[ \bar{x} = \frac{\sum{x_i · f_i}}{\sum{f_i}} \]
No caso da tabela, a média ponderada seria:
\[ \bar{x} = \frac{2 · 0 + 1 · 6 + 2 · 10 + 3 · 12 + 4 · 4}{2 + 6 + 10 + 12 + 4} = 2,3 \]
O valor médio 2,3 nesse caso sugere que o maior número de famílias tem 2 meninos e 2 meninas, sendo, porém, a tendência geral de uma leve superioridade numérica em relação ao número de meninos.
Média com dados agrupados: com intervalo de classe
Neste caso, convenciona-se que todos os valores incluídos em um determinado intervalo de classe coincidem com seu ponto médio.
Considere a distribuição:
| Altura (cm) | Frequência | Ponto médio |
|---|---|---|
| 151 - 155 | 8 | 153 |
| 156 - 160 | 11 | 158 |
| 161 - 165 | 13 | 163 |
| 166 - 170 | 1 | 168 |
A partir desse ponto segue como se não houvesse intervalos, sendo o valor para calcular a média ser o ponto médio:
\[ \bar{x} = \frac{8 · 153 + 11 · 158 + 13 · 163 + 1 · 168}{8 + 11 + 13 + 1} = 159,06 \]
Moda
> Denominamos moda o valor que ocorre com maior frequência em uma série de valores.
Como exemplo, o salário modal dos empregados de uma indústria é o salário mais comum, isto é, o salário recebido pelo maior número de empregados dessa indústria.
Moda com Dados não-agrupados
Quando se lida com dados não-agrupados, a moda é facilmente reconhecida: basta, de acordo com a definição, procurar o valor que mais se repete. Exemplo: 7, 8, 9, 10, 10, 10, 10, 11, 12, 13 e 15.
Mas existem casos que não haverá valor modal (amodal), isto é, nenhum valor apareça mais vezes que outros.
Em outros casos pode haver dois ou mais valores de concentração, o que é chamado de sério bimodal ou multimodal.
Moda com dados agrupados
Uma vez agrupados os dados, é possível determinar imediatamente a moda: basta fixar o valor da variável com maior frequência.
A classe que apresenta a maior frequência é denominada classe modal. Pela definição, podemos afirmar que a moda, neste caso, é o valor dominante que está compreendido entre os limites da classe modal.
O método mais simples para o cálculo de valor da moda consiste em tomar o ponto médio da classe modal o que denomina-se moda bruta.
Curvas de moda
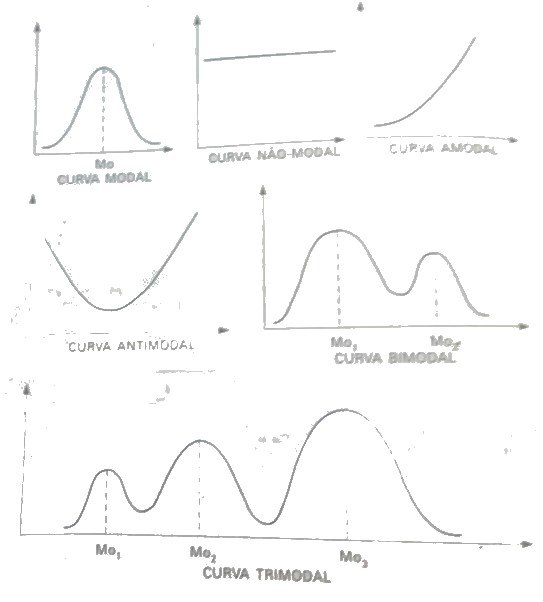
Porque usar moda ao invés de média
- Não é afetada pelos valores extremos da distribuição, desde que esses valores não constituam o valor modal
- É empregada quando desejamos obter uma medida rápida e aproximada de posição
- É empregada muito na estatística econômica e industrial
Mediana
> A mediana é outra medida de posição definida como o número que se encontra no centro de uma série de números, estando estes dispostos segundo uma ordem. Ela é tal que o número de observações com valores menores que a mediana é igual ao número de observações com valores maiores que a mediana.
Mediana com dados não agrupados
De uma série de dados: 5, 13, 10, 2, 18, 15, 6, 16, 9; o primeiro passo é a ordenação dos valores: 2, 5, 6, 9, 10, 13, 15, 16, 18.
Em seguida, toma-se aquele valor central que apresenta o mesmo número de elementos à direita e à esquerda. Caso a série tenha um número ímpar de dados isso será possível, como pode ser visto no exemplo que a mediana é 10. Caso a séria tenha um número par de dados se utiliza o ponto médio dos dois valores centrais da série.
Assim, se uma série for dos seguintes valores: 2, 6, 7, 10, 12, 13, 18, 21. Como o número de termos é par, se utiliza o ponto médio dos termos centrais: 10 e 12; tendo como mediana o valor 11.
Mediana com dados agrupados: sem intervalo de classe
Para o caso de dados agrupados, basta verificar a frequência acumulada imediatamente superior à metade da soma das frequências. A mediana será aquele valor da variável que corresponde a tal frequência acumulada.
| Nº de meninos | Frequência | Frequência acumulada |
|---|---|---|
| 0 | 2 | 2 |
| 1 | 6 | 8 |
| 2 | 10 | 18 |
| 3 | 12 | 30 |
| 4 | 4 | 34 |
\[ Md_{termo} = \frac{34}{2} = 17 \]
O termo de posição 17 se encontra na terceira linha porque a menor frequência acumulada que supera esse valor é 18, onde o valor que o corresponde é 2. Logo a mediana é igual a 2.
Nota-se que caso caso o termo seja um extremo superior de uma classe, no caso do exemplo seja 18, a mediana se dará pelo ponto médio entre as classes do termo e da classe superior a ele.
Mediana com dados agrupados: com intervalos de classe
| Altura (cm) | Frequência | Frequência acumulada |
|---|---|---|
| 151 - 155 | 8 | 8 |
| 156 - 160 | 11 | 19 |
| 161 - 165 | 13 | 32 |
| 166 - 170 | 1 | 33 |
Como o soma das frequências é 33, a mediana se encontra no valor 16,5. Neste caso, a classe que obtém o termo de ordem 17,5 é da classe 156-160, já que contém todos os termos entre 8 e 19. Denominamos essa classe de classe mediana.
A mediana é dada por uma regra de 3 dos valores possíveis dessa classe. Como são 13 elementos dentro da classe e a mediana será o termo 9,5 (17,5 - 8 termos da classe anterior), usa-se a seguinte fórmula:
\[ Md = \text{extremo inferior} + \text{amplitude da classe} *\frac{\text{número de termos para a mediana}}{\text{número de termos da classe}} \]
\[ Md = 156 + 4 · \frac{9,5}{13} = 158.92 \]
Porque usar mediana e não média
- Desejamos obter o ponto que divide a distribuição em partes iguais
- A variável em estudo é salário
- há valores extremos que afetam a média

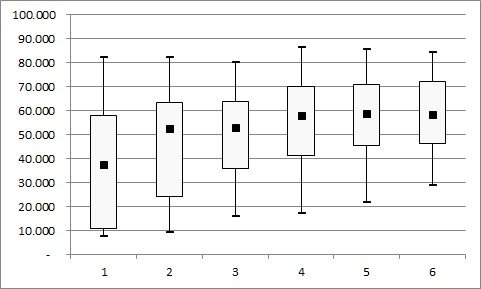
Outras medidas de posição
Similares à mediana, que se baseia na posição da série, existem os quartis, os percentis e os decis; que, juntos com a mediana, são conhecidos como separatrizes.
No caso dessas medidas de posição, a separação não é pelo número que se encontra no meio da série e sim do número que se encontra na posição 1/4 da série ou 1/10 da série etc...
Quartis são muito vistos em ações, por verificar o quanto os 25% piores ou melhores valores influenciam a ação.
Exercícios
Qual a soma dos desvios?
2) Considerando os conjuntos de dados:a. 3,5; 2,6 ; 5,9 ; 5,2 ; 8,6
b. 20,9; 7,2; 12,7; 20; 15,7
c. 51 ,6; 48,7; 50,3; 49,5; 48,9
d. 15; 18; 20; 13; 10; 16 ;14
Calcule:
I. a média
11. a mediana
111. a moda
3) Assinale a opção certa. A curva de frequência acumulada serve para calcular:a. a lei do acaso
b. a média.
c. a mediana.
d. a moda.
e. o desvio padrão.
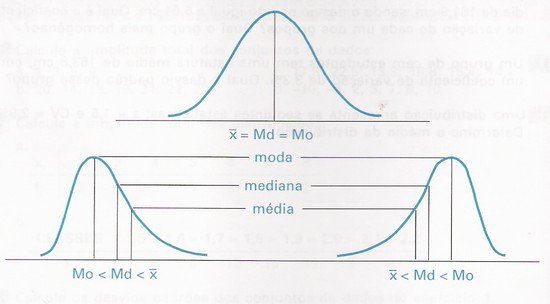
4) Assinale a opção certa. Uma curva simétrica se caracteriza pelo seguinte atributo:a. É assimétrica à esquerda.
b. A moda é maior que a mediana e a média.
c. A moda, a mediana e a média são iguais.
d. O desvio padrão é maior que a mediana e a moda.
e. Os decis são equivalentes à média.
5) Calcule a média aritmética, moda e mediana da seguinte distribuição:| Notas | Frequência |
|---|---|
| 0 - 2 | 5 |
| 2 - 4 | 8 |
| 4 - 6 | 14 |
| 6 - 8 | 10 |
| 8 - 10 | 7 |
| Estaturas (cm) | Frequência |
|---|---|
| 150 - 158 | 5 |
| 158 - 166 | 12 |
| 166 - 174 | 18 |
| 174 - 182 | 27 |
| 182 - 190 | 8 |
| Salários (R$) | Frequência |
|---|---|
| 500 - 700 | 18 |
| 700 - 900 | 31 |
| 900 - 1.100 | 15 |
| 1.100 - 1.300 | 3 |
| 1.300 - 1.500 | 1 |
| 1.500 - 1.700 | 1 |
| 1.700 - 1.900 | 1 |
| Pesos (kg) | Frequência |
|---|---|
| 145 - 151 | 10 |
| 151 - 157 | 9 |
| 157 - 163 | 8 |
| 163 - 169 | 6 |
| 169 - 175 | 3 |
| 175 - 181 | 3 |
| 181 - 187 | 1 |
| Avaliação do cliente | Frequência |
|---|---|
| 2 | 3 |
| 4 | 7 |
| 6 | 12 |
| 8 | 8 |
| 10 | 4 |
Gabarito
1) A soma dos desvios é sempre zero.
2) a. x = 5,1 ; Md = 5,2; não há Moda
b. x = 15.3 ; Md = 15,7; não há Moda
c. x = 49,8; Md = 49,5; não há Moda
d. x= 15,1; Md = 15; não há Moda
3) c.
4) c.
5) x = 5,3 ; Md = 5,3; Mo= 5
6) x = 172,4 ; Md = 174; Mo = 178
7) x = 843 ; Md = 810; Mo = 800
8) x = 159,4 ; Md = 157,8; Mo = 148
9) x = 6,17 ; Md = 6; Mo = 6












— Comentários 0
, Reações 1
Seja o primeiro a comentar