A Regressão Multivariada estende a regressão linear simples para mais de uma variável independente (X), permitindo modelar relações complexas onde múltiplos fatores influenciam uma variável dependente (Y).
Exemplo Prático. Prever o preço de uma casa (Y) com base em: Tamanho (X₁), Número de quartos (X₂) e Localização (X₃).
A equação geral é:
\[ Y = \beta_0 + \beta_1 X_1 + \beta_2 X_2 + \dots + \beta_k X_k + \epsilon \]
Onde:
- \( \beta_0 \): Intercepto (valor de Y quando todos X = 0).
- \( \beta_1, \beta_2, \dots, \beta_k \): Coeficientes de cada variável.
- \( \epsilon \): Erro aleatório. Valor esperado zero para os valores ótimos de \(\beta\)
Como Calcular os Coeficientes?
Método dos Mínimos Quadrados Ordinários (OLS). Minimiza a soma dos quadrados dos resíduos:
\[ \min \sum (Y_i - \hat{Y_i})^2 \]
Passo a Passo:1. Montar a Matriz de Projeto (X):
- Incluir uma coluna de 1's para o intercepto (\( \beta_0 \)).
- Exemplo para 3 variáveis:
\[ X = \begin{bmatrix} 1 & X_{11} & X_{12} & X_{13} \\ 1 & X_{21} & X_{22} & X_{23} \\ \vdots & \vdots & \vdots & \vdots \\ 1 & X_{n1} & X_{n2} & X_{n3} \end{bmatrix} \]
2. Calcular os Coeficientes:
\[ \beta = (X^T X)^{-1} X^T Y \]
- \( X^T \): Matriz transposta.
- \( (X^T X)^{-1} \): Matriz inversa.
Exercício Prático
| Tamanho (X₁) | Quartos (X₂) | Preço (Y) |
|---|---|---|
| 50 | 2 | 300 |
| 60 | 3 | 400 |
| 70 | 2 | 350 |
1. A equação de regressão multivariada.
2. O R² e interprete.
Problemas com Múltiplas Variáveis
1. Multicolinearidade: Quando as Variáveis se Confundem
A multicolinearidade ocorre quando duas ou mais variáveis independentes (X) estão altamente correlacionadas, tornando difícil distinguir seu impacto individual na variável dependente (Y).
Exemplo Prático. Suponha que queremos prever o preço de um carro (Y) usando: Idade do carro (X₁) e Quilometragem (X₂). Há um problema: idade e quilometragem estão fortemente relacionadas (carros mais velhos tendem a ter mais km). Isso infla a variância dos coeficientes, tornando as estimativas instáveis e difíceis de interpretar. Coeficientes podem ficar menores e instáveis, levando a conclusões erradas como "coeficiente X não é significativo" quando, na verdade, ele é importante, mas sua contribuição está sendo 'roubada' por outra variável correlacionada ("Quilometragem realmente impacta o preço, ou é só um efeito colateral da idade?").
Soluções: Remover Variáveis Redundantes (ex: escolher apenas "Idade" ou "Quilometragem"), para isso faça uma matriz de correlação entre as variáveis e verifique aquelas que possuem 80% ou mais de correlação. Ou transforme as variáveis em componentes normalizados usando técnicas como Análise de Componentes Principais (PCA), podendo 2 variáveis serem explicadas por 1 componente apenas.
Abaixo está uma terceira coluna que representa muito bem as duas primeiras, assim, você pode ignorar as duas primeiras colunas em sua regressão e fazer apenas com a terceira:
| Altura (cm) | Peso (kg) | PCA |
|---|---|---|
| 170 | 65 | -0.5 |
| 180 | 80 | 1.5 |
| 160 | 55 | -1.0 |
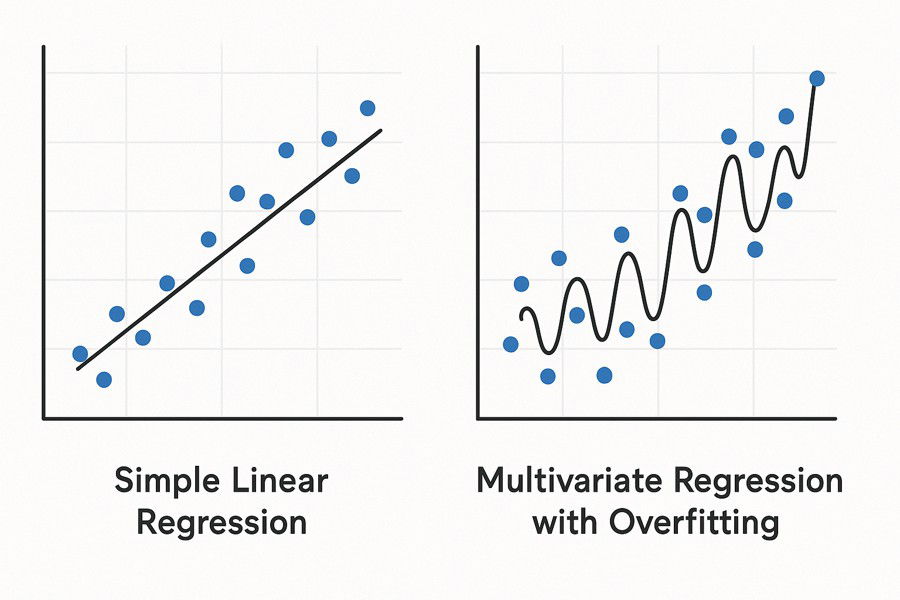
2. Overfitting (Sobreajuste): Quando o Modelo Decora os Dados
O overfitting ocorre quando o modelo se ajusta demais aos dados de treinamento, capturando até o "ruído" (variações aleatórias), e performando mal em dados novos.
Exemplo Prático: Prever notas de alunos (Y) com: Horas de estudo (X₁) , Número de lápis (X₂) e Cor da mochila (X₃) . Incluir "cor da mochila" (irrelevante) pode fazer o modelo memorizar padrões inexistentes, piorando a generalização. Quando o modelo atribui importância a fatores aleatórios (como a cor da mochila), ele perde capacidade de generalização e passa a performar mal em dados novos, já que essas "regras" inventadas não se repetem na realidade. Além disso, variáveis sem relação com o resultado diluem o impacto das variáveis verdadeiramente importantes, como horas de estudo. O modelo desperdiça energia tentando explicar ruído em vez de focar nos fatores que realmente influenciam as notas, tornando as previsões menos precisas e estáveis. Por isso, menos é mais: usar apenas variáveis relevantes garante um modelo mais simples, robusto e confiável.
Soluções: Divida os dados em partes, treine e teste em subconjuntos diferentes também chamado de Validação Cruzada (k-fold) . R² treino = 0.99, R² teste = 0.60 significa Overfitting. Ou remova variáveis não significativas (p-valor > 0.05). Calcule o AIC ou BIC para verificar se é necessário tantas variáveis.
O AIC (Critério de Informação de Akaike) e o BIC (Critério de Informação Bayesiano) são medidas estatísticas utilizadas para comparar a qualidade de ajuste de modelos, equilibrando a complexidade do modelo (número de parâmetros) e sua capacidade de explicar os dados. O AIC, desenvolvido por Hirotugu Akaike em 1974, é calculado pela fórmula \( AIC = 2k - 2\ln(L) \), onde \( k \) é o número de parâmetros e \( L \) é a verossimilhança máxima do modelo. Quanto menor o AIC, melhor o equilíbrio entre ajuste e simplicidade, penalizando modelos excessivamente complexos. Ele é amplamente usado em seleção de modelos, especialmente quando o objetivo é previsão, mas tende a favorecer modelos mais complexos em comparação ao BIC em amostras grandes. Já o BIC, também conhecido como Critério de Schwarz, foi proposto por Gideon Schwarz em 1978 e incorpora uma penalidade maior para o número de parâmetros, especialmente em amostras grandes. Sua fórmula é \( BIC = k\ln(n) - 2\ln(L) \), onde \( n \) é o tamanho da amostra. O BIC prioriza modelos mais simples e é mais rigoroso na seleção de parâmetros, sendo frequentemente preferido em contextos onde a verdadeira estrutura do modelo é desconhecida e busca-se evitar overfitting.
3. Dados Ausentes e Valores extremos: Quando os Dados Enganam
Mais variáveis significa ter mais probabilidade de ter que lidar com valores extremos ou com dados ausentes.
Os dados ausentes podem surgir por não resposta em pesquisas ou falhas técnicas, como sensores descalibrados. Por exemplo, num estudo médico onde 30% dos pacientes omitiram sua renda, essa lacuna pode enviesar análises. Para tratar esse problema, há duas abordagens principais: a exclusão de linhas incompletas (que só é válida quando os dados faltantes são aleatórios) e técnicas de imputação, como usar média/mediana para dados numéricos, regressão para estimativas baseadas em outras variáveis ou K-NN, que preenche valores com base em observações similares.
Valores extremos, como um salário de R$5 milhões numa amostra com média de R$10 mil, podem distorcer completamente os resultados do modelo. Esses valores extremos são identificáveis através de boxplots (pontos além de 1,5 vezes o intervalo interquartil) ou Z-scores (valores absolutos acima de 3). Para minimizar seu efeito, aplicam-se transformações logarítmicas ou Box-Cox que suavizam a disparidade, Winsorization (substituição pelo valor limítrofe mais próximo) ou, em casos justificáveis, a remoção direta. O tratamento adequado preserva a robustez do modelo sem perder informações críticas.
Exercício Prático
| Tamanho (m²) | Quartos | Idade (anos) | Preço (R$) |
|---|---|---|---|
| 50 | 2 | 5 | 300,000 |
| 60 | 3 | 10 | 400,000 |
| 70 | 2 | 3 | 350,000 |
| 80 | 4 | 15 | 200,000 |
1. Há multicolinearidade entre "Tamanho" e "Quartos"? Calcule a correlação.











— Comentários 0
, Reações 1
Seja o primeiro a comentar