Por que estudar matemática Financeira: valor do dinheiro no Tempo

Introdução à matemática financeira, noções de porcentagem, cálculos dos juros simples e compostos, descontos simples e composto, equivalência de capitais a juros, rendas certas e amortização de Empréstimos.

Para o aluno

- HAZZAN, Samuel; POMPEO, José Nicolau. Matemática financeira. Saraiva, 2007.

Para o professor

- GIMENES, Cristiano Marchi. Matemática financeira com Hp 12c e Excel. 2006.

- CÉSAR, Benjamin. Matemática Financeira: teoria e 700 questões. Ed. Campus, Rio de Janeiro–RJ, 5ª. Edição, 2005.

- CARVALHO, Sérgio; CAMPOS, Weber. Matemática Financeira Simplificada Para Concursos. 2010.

A Matemática Financeira visa estudar o valor do DINHEIRO no TEMPO. Tomando como cenário as aplicações de dinheiro e nos pagamentos de empréstimo.

Você se lembra quanto custava cada item a 30 anos atrás?

O dinheiro muda seu valor ao longo do tempo, o que deixa extremamente complicado comparar quantias de décadas atrás com quantias atuais. Geralmente o valor decai, isso é devido a inúmeros fatores. Denominamos essa queda de inflação. Inflação não necessariamente é ruim, ela é algo natural que ocorre na economia. Se o seu salário sobe acima ou igual à inflação não há pânico.

Inflação é até algo saudável quando comparamos com deflação. Um cenário de deflação significa que o salário de todos estão subindo mesmo estando parados. Para manter a balança, os salários costumam sofrer cortes. Corte salarial faz trabalhadores não ficarem contentes o que gera insatisfação e paralisação. Além disso, cenários de deflação significam que o consumidor está consumindo pouco ou que pode gerar ao longo prazo um problema econômico.

Apesar disso, inflações muito grandes também não são bem vindas. Cenários de hiperinflação traz incerteza e dificulta os empresários a pensar em cenários para a economia. Zimbabwe passou recentemente por hiperinflação:

Chamamos de CAPITAL qualquer valor monetário que uma pessoa(física ou jurídica) empresta para outra durante certo tempo. De um ponto de vista, também pode ser designado como valor inicial.

Tendo em vista que o emprestador abstém-se de usar o valor emprestado e ainda, em função da perda de poder aquisitivo do dinheiro pela inflação e do risco de tomar calote, surge o conceito de JURO.

JURO pode ser definido como o custo do empréstimo (para o tomador) ou a remuneração pelo uso do capital (para o emprestador).

Denominamos taxa de juros o valor do juro em uma certa unidade de tempo, expresso como uma PERCENTAGEM do capital.

Por último, ao final de uma ação financeira, a soma do capital com o juro é denominada MONTANTE, que é o valor final encontrado.

"Por cento" é o mesmo que "dividido por 100". E seu símbolo '%' lembra justamente um 100 misturado.

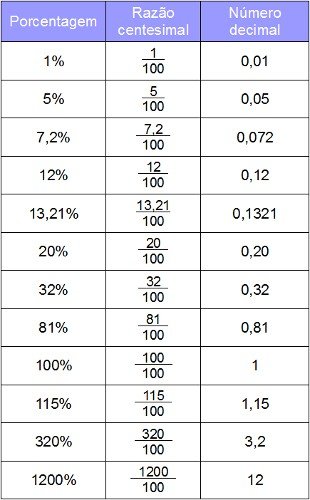
Todo número com exceção do irracional pode ser expresso em percentagem. O uso da percentagem se deve à facilidade de visualização dos valores por apenas ter que dividí-los por 100 (um processo fácil para seres humanos que utilizam o sistema de numeração decimal). Quais das abaixo é mais fácil perceber?

\[{1\over2} \text{ é o dobro de } {1\over4}\]

\[50\% \text{ é o dobro de } 25\%\]

A percentagem expressa uma proporção ou uma relação entre 2 (dois) valores, mantendo-se assim a proporcionalidade para comparação ao contrário do uso do valor nominal do dinheiro. Ao invés de sempre modificar o valor dos juros conforme o capital, usa-se percentagem por ser constante em sistemas diferentes e assim poder compará-los. Investir 1000 reais e ganhar 100 ou investir 500 reais e ganhar 60? O primeiro os juros são de 10% e no segundo de 12%. O uso de percentagem nesse caso deixa claro qual seria o melhor investimento!

A melhor forma de calcular a percentagem de um número é utilizando regra de três:

\[2\%\text{ de }300\]

\[{2\over100}={x\over300}\]

\[{x={2\over300*100}=6}\]

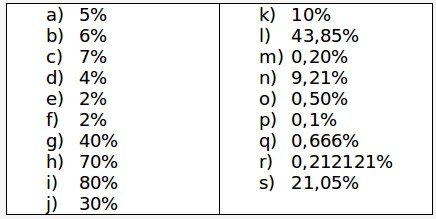
E1) Transforme em percentagem:

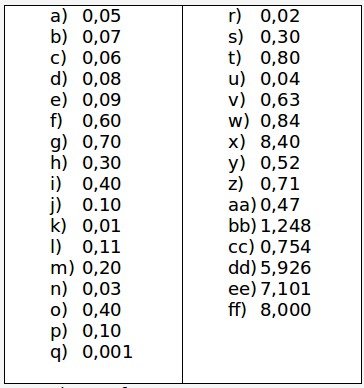
E2) Transforme em inteiro ou decimal, conforme o caso:

E3) Um capital de R$ 8000 é aplicado durante um ano à taxa de 22\% a.a. (22\% ao ano).

a) Qual o juro?

b) Qual o montante?