Assimetria em distribuições
Quando uma distribuição é simétria, a média e a moda coincidem. sendo a distribuição assimétria à esquerda ou negativa, a média é menor que a moda; e sendo assimétrica à direita ou positiva, a média é maior que a moda.
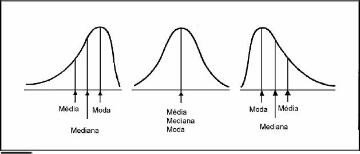
Assim:
\[ \bar{x} - Mo = 0 \text{--> assimetria nula ou distribuição simétrica} \]
\[ \bar{x} - Mo < 0 \text{--> assimetria negativa ou à esquerda} \]
\[ \bar{x} - Mo > 0 \text{--> assimetria positiva ou à direita} \]
Tipos de assimetria
Quais frequências abaixo são simétricas?
| classes | Frequência |
|---|---|
| 2-6 | 6 |
| 6-10 | 12 |
| 10-14 | 24 |
| 14-18 | 12 |
| 18-22 | 6 |
Temos:
\[ \bar{x} = 12 \]
\[ Md = 12 \]
\[ Mo = 12 \]
\[ s = 4,42 \]
Logo, a distribuição é simétrica.
| classes | Frequência |
|---|---|
| 2-6 | 6 |
| 6-10 | 12 |
| 10-14 | 24 |
| 14-18 | 30 |
| 18-22 | 6 |
Temos:
\[ \bar{x} = 12,9 \]
\[ Md = 13,5 \]
\[ Mo = 16 \]
\[ s = 4,20 \]
Logo, a distribuição é assimétrica negativa.
| classes | Frequência |
|---|---|
| 2-6 | 6 |
| 6-10 | 30 |
| 10-14 | 24 |
| 14-18 | 12 |
| 18-22 | 6 |
Temos:
\[ \bar{x} = 11,1 \]
\[ Md = 10,5 \]
\[ Mo = 8 \]
\[ s = 4,20 \]
Logo, a distribuição é assimétrica positiva.
Coeficiente de assimetria
A medida de assimetria anterior, por ser absoluta, apresenta a mesma deficiência do desvio padrão, isto é, não permite comparações com outras distribuições a fim de discutir se uma é mais assimétrica do que outra.
Para comparações, é utilizado o coeficiente de assimetria de Pearson:
\[ As = \frac{3 · (\bar{x} - Md)}{s} \]
Dos exemplos anteriores:
\[ As_1 = \frac{3 · (12-12)}{4,42} = 0 \]
\[ As_2 = \frac{3 · (12,9-13,5)}{4,20} = -0,429 \]
\[ As_3 = \frac{3 · (11,1 - 10,5)}{4,20} = 0,429 \]
Curtose
> Denominamos curtose o grau de achatamento em relação a uma distribuição padrão normal.
A curtose indica o quão concentrados os dados estão ao redor da média. Ela nos diz se a curva é mais "pontuda" ou "achatada" em comparação com a normal.
| Tipo de curtose | Nome técnico | Características |
|---|---|---|
| Alta | Leptocúrtica | Pico alto e caudas longas – mais dados concentrados na média, mas muitos valores extremos. |
| Normal | Mesocúrtica | Formato semelhante ao da curva normal. |
| Baixa | Platicúrtica | Curva achatada – dados mais dispersos, poucos extremos. |
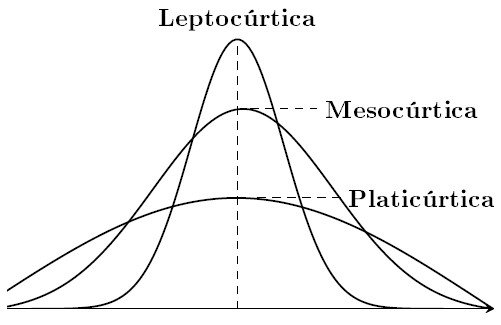
Exemplos:
1. Uma distribuição de notas com muitos alunos com média próxima a 7, mas também muitos com nota 0 ou 10 → Leptocúrtica
2. Uma distribuição de altura com pouca variação entre os indivíduos → Mesocúrtica
3. Uma distribuição de idade onde todas as faixas etárias aparecem com frequência semelhante → Platicúrtica
Coeficiente de Curtose (excesso de curtose)
A curtose pode ser quantificada da seguinte forma:
\[ K = \frac{ \sum (x_i - \bar{x})^4 }{n s^4} \]
A medida padrão da curtose de uma distribuição, originada por Karl Pearson, é uma versão em escala do quarto momento da distribuição. Esse número está relacionado às caudas da distribuição, não ao seu pico; portanto, a caracterização, às vezes vista, da curtose como "pico" é incorreta. Para essa medida, uma curtose mais alta corresponde à maior extremidade dos desvios (ou outliers), e não à configuração dos dados próxima à média.
Mas usamos com mais frequência o excesso de curtose, definido como:
\[ \text{Curtose excessiva} = K - 3 \]
- Se \( K - 3 > 0 \): Leptocúrtica
- Se \( K - 3 = 0 \): Mesocúrtica
- Se \( K - 3 < 0 \): Platicúrtica
O valor 3 representa a curtose da distribuição Normal, logo este é o valor utilizado como padrão para comparação.
Boxplot ou Diagrama de Caixa para verificar Assimetria e Curtose
Desenvolvido por John Tukey em 1970, o boxplot é uma representação visual que resume a distribuição de um conjunto de dados através de cinco medidas-resumo: mínimo, primeiro quartil (Q1), mediana, terceiro quartil (Q3) e máximo. Sua simplicidade gráfica permite uma análise rápida e eficiente da dispersão, assimetria e valores atípicos dos dados.

Elementos do Boxplot:
- Caixa: Representa o intervalo interquartílico (IQR = Q3 - Q1), contendo 50% dos dados centrais
- Linha da mediana: Divide a caixa em duas partes, indicando o centro da distribuição
- Bigodes (whiskers): Extendem-se até 1,5 × IQR abaixo de Q1 e acima de Q3
- Valores atípicos: Pontos além dos bigodes, indicando observações extremas
O boxplot é uma ferramenta excepcional para avaliar visualmente a assimetria de uma distribuição porque sua estrutura revela imediatamente o posicionamento relativo da mediana (a linha dentro da caixa) e a simetria dos quartis. Em uma distribuição simétrica, a mediana estará aproximadamente no centro da caixa, e os comprimentos dos "bigodes" (whiskers) superior e inferior serão semelhantes. Já uma assimetria é identificada de forma intuitiva: se a mediana estiver mais próxima da parte inferior da caixa (Q1) e o bigode superior for consideravelmente mais longo que o inferior, a distribuição é assimétrica à direita (positiva). Inversamente, se a mediana estiver próxima do topo da caixa (Q3) e o bigode inferior for mais longo, a assimetria é à esquerda (negativa). Essa representação visual dos quartis e da extensão das caudas fornece uma compreensão imediata e robusta da simetria dos dados, sem a necessidade de cálculos complexos.

Além da assimetria, o boxplot oferece insights valiosos sobre a curtose, que se relaciona com o "achatamento" da distribuição e o peso das caudas. Uma caixa compacta (com um Intervalo Interquartílico - IQR - pequeno) combinada com bigodes muito longos indica uma distribuição leptocúrtica, onde os dados estão altamente concentrados em torno do centro, mas possuem caudas pesadas e longas, com presença de valores extremos. Por outro lado, uma caixa larga (IQR grande) e bigodes curtos sugerem uma distribuição platicúrtica, onde os dados estão mais espalhados e não há valores extremamente distantes do centro. Dessa forma, a combinação da proporção entre a largura da caixa e o comprimento dos bigodes, junto com a detecção de outliers, permite uma inferência clara sobre a curtose e a natureza geral da distribuição, tornando o boxplot uma ferramenta poderosa para a análise exploratória de dados.
Montando o Boxplot
Vamos usar os seguintes números, já ordenados:
1, 2, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39Coloque em ordem seus dados
Os dados já estão em ordem crescente.
Encontrar a Mediana (Q2)
Como temos 40 números (n = 40, par), a mediana será a média dos dois valores centrais:
- Posições centrais: 20ª e 21ª
- Valores: 19 e 20
- Mediana (Q2) = (19 + 20) / 2 = 19.5
Encontrar o Primeiro Quartil (Q1)
Q1 é a mediana da primeira metade dos dados (primeiros 20 números):
- Primeira metade: 1, 2, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19
- Mediana dos primeiros 20: média do 10º e 11º valores
- Valores: 9 e 10
- Q1 = (9 + 10) / 2 = 9.5
Encontrar o Terceiro Quartil (Q3)
Q3 é a mediana da segunda metade dos dados (últimos 20 números):
- Segunda metade: 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39
- Mediana dos últimos 20: média do 10º e 11º valores dessa metade
- Valores: 29 e 30
- Q3 = (29 + 30) / 2 = 29.5
Calcular o Intervalo Interquartil (IQR)
IQR = Q3 - Q1 = 29.5 - 9.5 = 20Calcular os Limites para Identificar Outliers
- Limite Inferior = Q1 - 1.5 × IQR = 9.5 - 1.5 × 20 = 9.5 - 30 = -20.5
- Limite Superior = Q3 + 1.5 × IQR = 29.5 + 1.5 × 20 = 29.5 + 30 = 59.5
Identificar Valores Atípicos (Outliers)
Verificar se algum valor está abaixo de -20.5 ou acima de 59.5:
- Valor mínimo nos dados: 1
- Valor máximo nos dados: 39
- Não há outliers neste conjunto, pois todos os valores estão dentro do intervalo [-20.5, 59.5].
Encontrar os Bigodes (Whiskers)
- Bigode inferior: menor valor dentro do limite inferior → 1
- Bigode superior: maior valor dentro do limite superior → 39
Construir o Boxplot
Agora temos todas as medidas:
- Mínimo: 1
- Q1: 9.5
- Mediana (Q2): 19.5
- Q3: 29.5
- Máximo: 39
Desenho esquemático:0 5 10 15 20 25 30 35 40
|----|----|----|----|----|----|----|----|
|---------|__________|---------|
Q1(9.5) Med(19.5) Q3(29.5)
Bigode: de 1 a 9.5 e de 29.5 a 39
Exercícios
1) Considere os seguintes resultados relativos a três distribuições de frequência:
| Distribuições | média | Moda |
|---|---|---|
| A | 52 | 52 |
| B | 45 | 50 |
| C | 48 | 46 |
Determine o tipo de assimetria de cada uma delas.
2) Uma distribuição de frequência apresenta as seguintes medidas: média = 48,1; mediana = 47,9; e desvio padrão = 2,12. Calcule o coeficiente de assimetria de Pearson.
3) Em uma distribuição de frequência foram encontradas as seguintes medidas:
Média = 33,18; moda = 27,50; mediana = 31,67; e desvio padrão = 12,25.
a. Classifique o tipo de assimetria.
b. Calcule o coeficiente de assimetria de Pearson.
4. Uma distribuição tem Curtose = 4,5. Classifique a distribuição (platicúrtica, mesocúrtica ou leptocúrtica).
5. Explique com suas palavras o que significa uma distribuição leptocúrtica com assimetria negativa.
6. Monte o Boxplot para o seguinte conjunto: [12, 14, 19, 22, 23, 25, 27, 29, 31, 34, 35, 37, 39, 42, 44, 45, 48, 51, 53, 56, 59, 61, 63, 66, 67, 68, 71, 74, 77, 78, 79, 82, 85, 86, 88, 91, 93, 95, 97]
7. Monte o Boxplot para o seguinte conjunto: [-15, 5, 29, 31, 32, 33, 35, 36, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 57, 58, 59, 60, 61, 62, 63, 64, 65, 67, 88, 120, 150]












— Comentários 0
, Reações 1
Seja o primeiro a comentar