O que é inferência estatística
A palavra inferência tem, para este contexto, o significado de conclusivo. Para inferência estatística, queremos obter conclusões sobre nosso conjunto de dados a partir de modelos.
A inferência estatística faz proposições sobre um universo, usando dados tirados de uma amostragem. Dada um hipótese sobre um universo, para o qual nós queremos tirar inferências, a inferência estatística consiste em (primeiramente) selecionar um modelo estatístico do processo que gera os dados e (segundamente) deduzir as proposições a partir do modelo.
Uma das ferramentas mais importantes na inferência estatística é o intervalo de confiança (IC), que fornece uma faixa de valores que provavelmente contém o parâmetro populacional verdadeiro, como a média ou a proporção. O intervalo de confiança não apenas estima o parâmetro, mas também expressa a incerteza associada a essa estimativa.
Nesta aula, exploraremos o conceito de intervalo de confiança, como ele é construído e interpretado, além de suas aplicações em diversas áreas.
Quando utilizar Intervalo de Confiança
Intervalos de confiança são usados para indicar a confiabilidade de uma estimativa. Por exemplo, um IC pode ser usado para descrever o quanto os resultados de uma pesquisa são confiáveis. Sendo todas as estimativas iguais, uma pesquisa que resulte num IC pequeno é mais confiável do que uma que resulte num IC maior.
Podemos interpretar o intervalo de confiança como um intervalo que contém os valores "plausíveis" que a média da população pode assumir. Assim, a amplitude do intervalo está associada a incerteza que temos a respeito do parâmetro.
Vamos entender esse intervalo com um exemplo: qual a média de um lançamento de um dado de 6 faces? A média é 3,5, em outras palavras, a população tem média 3,5. Agora, imagina que lançando um dado 5 vezes coletamos os seguintes dados:
\[ 1,6,3,2,1 \]
A média da amostra é 2,6!!
Agora lançamentos de novo 5 dados:
\[ 5,3,6,3,1 \]
Dessa vez a média da amostra é 3,83!!
Simulações com a média amostral
E se começarmos a guardar esse resultado da média? Vamos fazer algumas simulações:
Simulações para amostra de tamanho 5
Para 10 grupos de 5 lançamentos de dados (amostra tamanho 5)
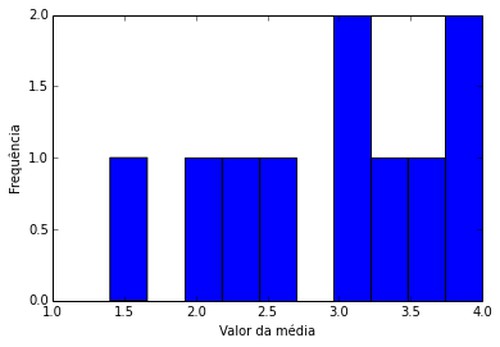
Para 30 grupos de 5 lançamentos de dados (amostra tamanho 5)
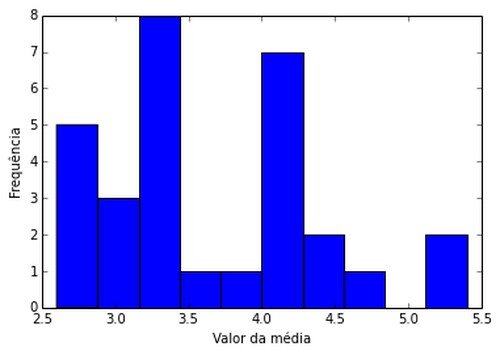
Para 70 grupos de 5 lançamentos de dados (amostra tamanho 5)
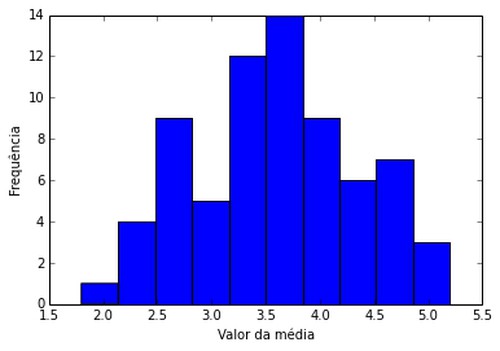
Para 200 grupos de 5 lançamentos de dados (amostra tamanho 5)
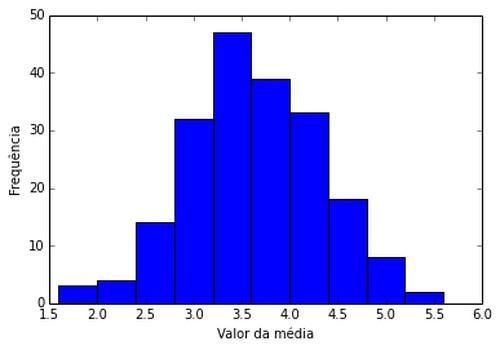
Para 2000 grupos de 5 lançamentos de dados (amostra tamanho 5)
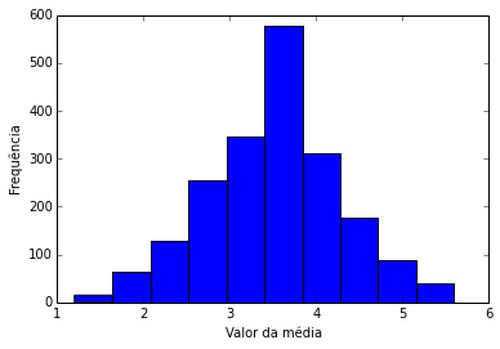
Depois de uma certa quantidade é possível verificar uma curva normal ocorrendo. Mas demorou para a curva normal aparecer, logo, vamos fazer uma mudança, e se usarmos uma amostra de tamanho 200? Isto é, vamos ver a média depois de lançar 200 dados, espera-se que a média fique em volta de 3,5 como é da população! Vamos para as simulações:
Simulações para amostra de tamanho 200
Para 10 grupos de 200 lançamentos de dados (amostra tamanho 5)
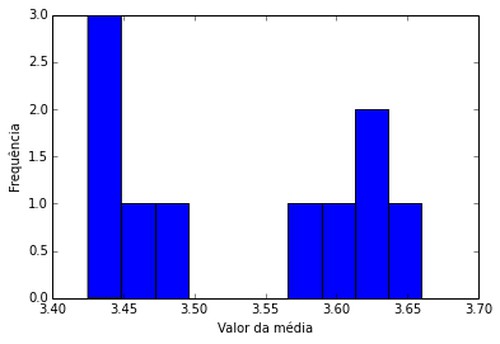
Para 70 grupos de 200 lançamentos de dados (amostra tamanho 5)
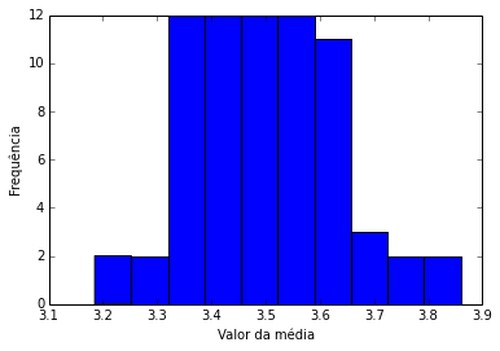
Para 200 grupos de 200 lançamentos de dados (amostra tamanho 5)
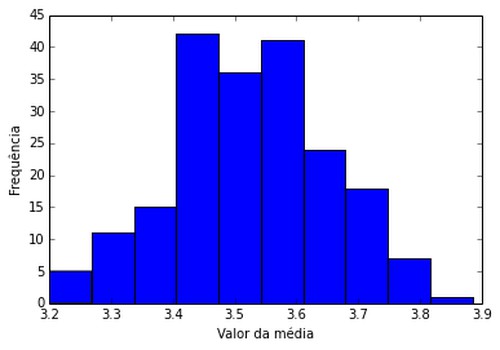
Para 2000 grupos de 200 lançamentos de dados (amostra tamanho 5)
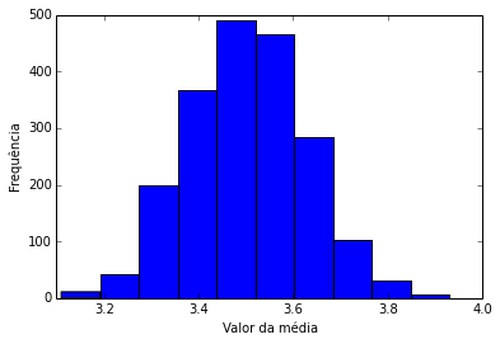
De novo o gráfico é similar a uma normal!
Conclusões sobre as simulações
Percebe-se dois pontos:
O gráfico é similar à normal. No caso usaremos a teoria central do limite de novo: Em repetidos experimentos, a média de uma amostra irá tender a uma distribuição normal.
A amplitude do primeiro é diferente da amplitude do segundo. Lidando com amostras, quanto maior sua amostra, menor o desvio padrão da média amostral.
Média amostral
Assim, dizemos que a média amostral é normalmente distribuída. A variância da média amostral é a variância da população dividida pelo tamanho da amostra:
\[ \text{Var}(\bar{X}) = \frac{\sigma^2}{n} \]
Ela é dependente da média da amostra e o desvio padrão da amostra dividido pela raiz do tamanho da amostra.
\[ \bar{X} \sim N\left(\mu, \frac{\sigma^2}{n}\right) \]
A significância no intervalo de confiança da média amostral
O tamanho do intervalo é definido pela distribuição normal da média amostral e da confiança escolhida. Por exemplo, é comum usar para estes cálculos 95% de confiança, isso quer dizer que em 95% das vezes a média da população estará neste intervalo. A confiança é inversamente proporcional à significância, a significância está ligada ao erro do teste, neste caso, uma confiança de 95% significa uma significância de 5%.
No caso, essa confiança é denominada alpha e procuramos um intervalo em que a média populacional estará abrangendo a confiança dada:
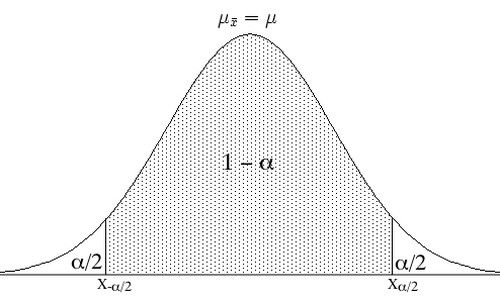
Assim, dado o nível de confiança que gostaria de ter: 90%, 95%, 98%, 99% etc... irá procurar os pontos que possibilitam ter um intervalo com essa confiança. Em intervalos bicaudais, um intervalo que tende para direita quanto para esquerda, procuramos os pontos onde deixem a probabilidade de erro metade para esquerda e metade para direita.
Logo, temos como limite inferior (a):
\[ a = \bar{X} - z *\frac{\sigma}{\sqrt{n}} \]
E limite superior (b):
\[ b = \bar{X} + z *\frac{\sigma}{\sqrt{n}} \]
Com estes dois pontos podemos montar um intervalo que representa onde a média da população provavelmente se encontra.
Exemplo real
Uma pesquisa de opinião entrevistou 2500 pessoas com respeito se irão votar ou não votar num candidato A. Em média, 20% dos entrevistados votarão no candidato A e sabemos que o desvio padrão populacional é de 40%, já que o desvio amostral é de 40% e temos uma amostra muito grande(mais de 2000 pessoas). Uma empresa de consultoria quer construir um intervalo de confiança para a média populacional, em outras palavras, poder, a partir dessa amostra, definir quantas pessoas vão votar no candidato A na população total. Para isso definiu que haverá 5% significância ou 95% de confiança seu intervalo.
Um intervalo de 95% de confiança bicaudal indica que haverá 2,5% de erro à direita e à esquerda. Sabendo que a média de uma amostra se comporta como uma normal, o Z que estabelece o erro de 2,5% à esquerda é de -1,96 e o Z que estabelece erro de 2,5% à direita é de 1,96. Em resumo:
\[ −1,96<\text{nosso intervalo na normal reduzida}<1,96 \]
No caso é na normal reduzida. Devemos assim transformá-la para a normal da questão que possui 20% de média.
\[ P(X<2,5\%)=20\%−1,96∗\frac{40\%}{√2500}=18,43\% \]
\[ P(X>97,5\%)=20\%+1,96∗\frac{40\%}{√2500}=21,56\% \]
O que aconteceria se utilizarmos os mesmos parâmetros do exercício anterior, mas 40% dos entrevistados vão votar no candidato A com desvio padrão populacional de 24%?
\[ P(X<2,5\%)=40\%−1,96∗\frac{24\%}{√2500}=39,05\% \]
\[ P(X>97,5\%)=40\%+1,96∗\frac{24\%}{√2500}=40,94\% \]
O que aconteceria se utilizarmos os mesmos parâmetros do exercício anterior, mas com significância de 2%?
Significância de 2% significa que ignoraremos os 1% de média inferiores ou os 1% maiores médias:
\[ P(X<1\%)=40\%−2,33∗\frac{24\%}{√2500}=38,88\% \]
\[ P(X>99\%)=40\%+2,33∗\frac{24\%}{√2500}=41,11\% \]
Exercícios
1) Se uma amostra aleatória n=25, tem uma média amostral de 51,3 e uma desvio padrão populacional de σ=2. Construa o intervalo com 95% de confiança para a média populacional µ.
2) Sabe-se que a vida em horas de um bulbo de lâmpada de 75W é distribuída de forma aproximadamente normal com desvio padrão de σ=25. Uma amostra aleatória de 20 bulbos tem uma vida media de 1.014 horas. Construa um intervalo de confiança de 95% para a vida média.
3) Qual deve ser o tamanho da amostra para que o intervalo com 99,5% de confiança para a média populacional tenha uma semi amplitude não superior a 1,5? Sabe-se que a variância populacional é de 23.
4) Qual deve ser o tamanho de uma amostra cujo desvio padrão é 10 para que a diferença da média amostral para a média da população, em valor absoluto, seja menor que 1, com coeficiente de confiança igual a:
a) 95%
b) 99%
5) Uma variável aleatória X tem distribuição normal, com média amostral 100 e desvio padrão populacional 10. Se o tamanho amostral é de 16 elementos, calcule P(90 < média populacional < 110).
6) Que tamanho deveria ter uma amostra com média amostral de 100 e desvio padrão populacional 10 para que P(90 < média populacional < 110) = 95%?
7) Uma amostra aleatória de 625 donas de casa revela que 70% da amostra preferem a marca A de detergente com desvio padrão populacional de 45%. Construir um intervalo de confiança para p = proporção das donas de casa que preferem A com coeficiente de confiança γ = 90%.
8) Suponha que estejamos interessados em estimar a porcentagem de consumidores de um certo produto. Se a amostra de tamanho 300 forneceu 100 indivíduos que consomem o dado produto, determine o intervalo de confiança da média populacional, com c.c. de 95%; interprete o resultado. (Desvio padrão de proporção pode ser calculado pela fórmula: p x ( 1 − p ))
Gabarito
1) I.C. = 51,3 ± 0,78;
2) I.C. = 1014 ± 11;
3) 81;
4) a) 385; b) 665;
5) Quase 100%;
6) Aproximadamente 4.
7) (0.6692 ; 0.7308).
8) (0.280; 0.387).












— Comentários 0
, Reações 1
Seja o primeiro a comentar