O que é o Solver?
O Solver é uma ferramenta poderosa no Excel que permite otimizar um modelo matemático. Ele pode encontrar valores ideais para um conjunto de variáveis, respeitando as restrições impostas, seja para maximizar ou minimizar um resultado.
Exemplos típicos de uso:
- Minimizar custos de produção;
- Maximizar lucros;
- Encontrar a combinação ideal de produtos a serem fabricados com recursos limitados.
Exemplo 1: Maximização de Lucros
Problema:
Uma pequena fábrica de móveis produz cadeiras e mesas. Cada cadeira gera um lucro de R$ 30, enquanto cada mesa gera R$ 50. A fábrica tem 100 horas de trabalho disponíveis por semana, com cada cadeira consumindo 10 horas e cada mesa 20 horas. Qual a combinação de cadeiras e mesas que maximiza o lucro, respeitando o limite de horas?
Passo a Passo no Excel:
Configuração do problema:
Variáveis de decisão: número de cadeiras e mesas a produzir.
Função objetivo: maximizar o lucro total.
Restrições: não ultrapassar 100 horas de trabalho.
Criar o modelo no Excel:
Em uma célula, defina as quantidades de cadeiras e mesas (ex.: C2 para cadeiras e D2 para mesas).
Em outra célula, insira a fórmula do lucro total: =C230 + D250.
Em outra célula, insira a fórmula do tempo total de trabalho: =C210 + D220.
Configurar o Solver:
Vá até a aba Dados e clique em Solver.
Em "Definir Objetivo", selecione a célula que calcula o lucro.
Marque a opção Maximizar.
Em "Células Variáveis", selecione as células de quantidades de cadeiras e mesas.
Em "Restrições", adicione que o tempo total de trabalho não pode exceder 100 horas. Também adicione que as cadeiras, tempo e mesas devem ser maior que 0.
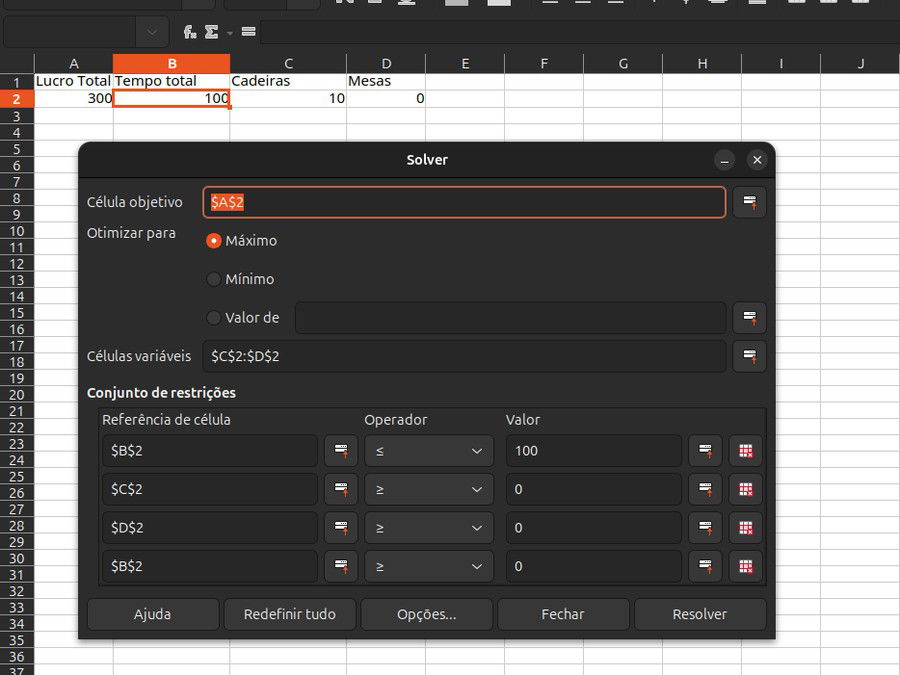
Clique em Resolver e veja os resultados. O Excel mostrará quantas cadeiras e mesas a fábrica deve produzir para maximizar o lucro sem ultrapassar o tempo disponível. A sua tela deve estar assim neste momento:
Exemplo 2: Minimização de Custos de Transporte
Uma empresa de logística quer minimizar os custos de transporte de dois armazéns (A1 e A2) para três lojas (L1, L2, L3). Cada armazém tem uma capacidade limitada de produtos, e cada loja tem uma demanda específica. Os custos de transporte variam de acordo com a rota entre cada armazém e loja.
A pergunta é: como a empresa pode minimizar os custos totais de transporte enquanto atende às demandas das lojas e respeita as capacidades dos armazéns?
Dados:
Capacidade dos armazéns:
Armazém A1: 100 unidades.
Armazém A2: 150 unidades.
Demanda das lojas:
Loja L1: 80 unidades.
Loja L2: 70 unidades.
Loja L3: 100 unidades.
Custo de transporte (R$/unidade):
| L1 | L2 | L3 | |
|---|---|---|---|
| A1 | 4 | 6 | 8 |
| A2 | 5 | 3 | 7 |
O objetivo é minimizar o custo de transporte, garantindo que a quantidade enviada de cada armazém não exceda sua capacidade e que todas as lojas recebam exatamente a quantidade de produtos que precisam.
Passo a Passo no Excel:
Em uma planilha, crie uma tabela com os custos de transporte de cada armazém para cada loja.
Adicione linhas extras para as capacidades dos armazéns e as demandas das lojas.
Capacidades dos armazéns:
A1: 100 unidades.
A2: 150 unidades.
Demandas das lojas:
L1: 80 unidades.
L2: 70 unidades.
L3: 100 unidades.
Definir as variáveis de decisão:
Crie células para representar as quantidades enviadas de cada armazém para cada loja. Você pode organizar assim:
| L1 | L2 | L3 | |
|---|---|---|---|
| A1 | Q1 | Q2 | Q3 |
| A2 | Q4 | Q5 | Q6 |
Onde:
Q1 é a quantidade enviada de A1 para L1;
Q2 é a quantidade enviada de A1 para L2;
Q3 é a quantidade enviada de A1 para L3;
Q4 é a quantidade enviada de A2 para L1;
Q5 é a quantidade enviada de A2 para L2;
Q6 é a quantidade enviada de A2 para L3.
Criar a função objetivo (Minimização de Custos):
Em outra célula, calcule o custo total de transporte com base nas quantidades enviadas e nos custos por unidade:
Custo total = Q14 + Q26 + Q38 + Q45 + Q53 + Q67
Adicionar as restrições:
Agora, você precisa adicionar restrições ao problema. Essas restrições incluem:
As quantidades enviadas de cada armazém não podem ultrapassar suas capacidades.
Total enviado de A1 = Q1 + Q2 + Q3 ≤ 100.
Total enviado de A2 = Q4 + Q5 + Q6 ≤ 150.
As lojas precisam receber exatamente a quantidade que demandam.
Total recebido por L1 = Q1 + Q4 = 80.
Total recebido por L2 = Q2 + Q5 = 70.
Total recebido por L3 = Q3 + Q6 = 100.
Configurar o Solver:
Vá até a aba Dados no Excel e clique em Solver.
Objetivo: selecione a célula que contém o custo total de transporte.
Tipo de otimização: escolha Minimizar, pois estamos tentando minimizar o custo total.
Variáveis de decisão: selecione as células que representam as quantidades enviadas de cada armazém para cada loja (Q1 a Q6).
Restrições: adicione as seguintes:
Quantidade enviada de cada armazém não pode exceder sua capacidade.
Cada loja deve receber exatamente a quantidade que demanda.
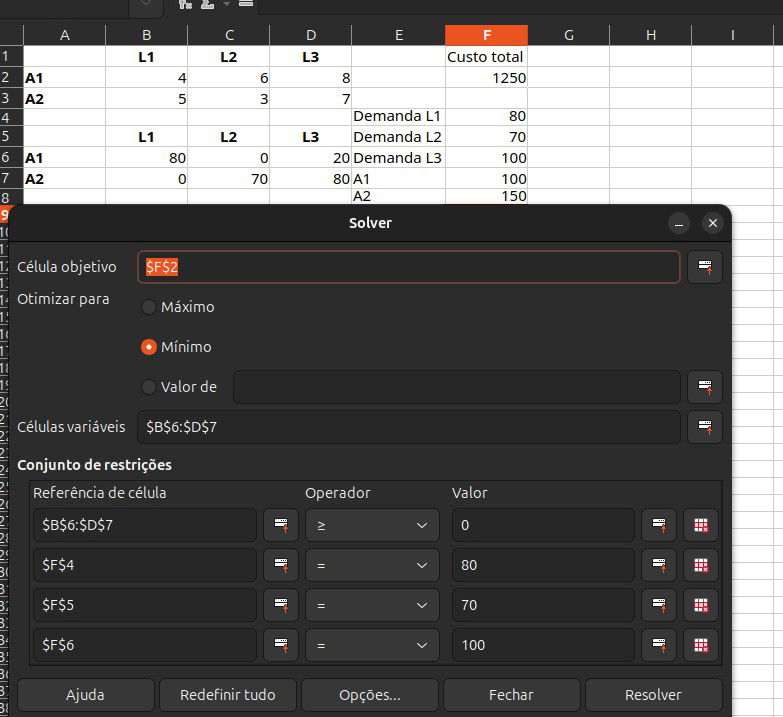
Clique em Resolver e o Solver encontrará a combinação de quantidades que minimiza o custo de transporte, respeitando todas as restrições. Deve ficar assim a sua tela:
Exercícios
1) Maximização de Produção
Você gerencia uma padaria que produz dois tipos de pães: integral e branco. Cada pão integral gera R$ 2 de lucro, e cada pão branco gera R$ 1,50. A padaria tem 200 quilos de farinha disponíveis por dia. Cada pão integral consome 0,5 kg de farinha, enquanto cada pão branco consome 0,25 kg. Use o Solver para determinar a quantidade ideal de cada tipo de pão a ser produzida para maximizar o lucro.
Função objetivo: maximizar o lucro total.
Restrições: não usar mais de 200 kg de farinha.
2) Minimização de Tempo
Uma empresa fabrica dois tipos de produtos: A e B. O produto A requer 5 horas de trabalho e o produto B requer 3 horas. A empresa tem 152 horas disponíveis e deseja trabalhar exatamente neste tempo de produção. Como configurar o Solver para encontrar a combinação ideal de produtos, garantindo que sejam produzidas pelo menos 10 unidades de cada?
Função objetivo: o tempo total de produção ser igual a 152.
Restrições: pelo menos 10 unidades de cada produto.
3) Maximização de Produção com Lucro Fixo
Uma empresa fabrica dois produtos, A e B, e precisa obter um lucro fixo de R$ 4.000. O produto A gera R$ 100 de lucro por unidade, enquanto o produto B gera R$ 150 por unidade. O tempo de produção disponível é de 200 horas, com o produto A consumindo 5 horas por unidade e o produto B consumindo 8 horas. Use o Solver para determinar quantas unidades de cada produto devem ser fabricadas para alcançar o lucro fixo de R$ 4.000, minimizando o tempo de produção.
Função objetivo: minimizar o tempo de produção.
Restrições:
Lucro total = R$ 4.000.
Tempo de produção disponível = 200 horas.
4) Alocação de Recursos
Uma empresa de marketing digital tem três tipos de campanhas (C1, C2 e C3) que deseja rodar em uma plataforma de anúncios. A empresa tem um orçamento de R$ 10.000 e quer maximizar o retorno sobre o investimento (ROI). A campanha C1 tem um ROI de 5%, a campanha C2 tem um ROI de 8% e a campanha C3 tem um ROI de 10%. Cada campanha tem um valor mínimo de investimento: C1 = R$ 2.000, C2 = R$ 3.000, e C3 = R$ 1.000. Use o Solver para determinar como distribuir o orçamento de forma a maximizar o ROI total.
Função objetivo: maximizar o ROI total.
Restrições:
Orçamento total = R$ 10.000.
Respeitar os valores mínimos de investimento para cada campanha.
5) Custo Fixo de Transporte
Uma empresa precisa enviar produtos de dois armazéns (A1 e A2) para três lojas (L1, L2 e L3). O custo por unidade é o seguinte:
| L1 | L2 | L3 | |
|---|---|---|---|
| A1 | 8 | 6 | 8 |
| A2 | 7 | 4 | 6 |
A empresa quer garantir que todas as lojas recebam suas quantidades específicas de produtos sem ultrapassar as capacidades dos armazéns. A ideia é garantir que o custo total de transporte seja o menor possível. Como configurar o Solver para encontrar a solução ideal de distribuição?
Função objetivo: custo total menor possível
Restrições:
As lojas L1, L2 e L3 devem receber exatamente 200, 150 e 100 unidades, respectivamente.
O total de unidades enviadas de A1 e A2 não deve ultrapassar suas capacidades de 250 e 200 unidades, respectivamente.
6) Planejamento de Horas de Trabalho
Você é gerente de uma empresa de consultoria e precisa alocar horas de trabalho para dois tipos de tarefas: análise de dados e relatórios. O tempo disponível para trabalho é de 120 horas por semana, e você deseja maximizar o número de tarefas concluídas. Cada tarefa de análise de dados consome 4 horas e cada tarefa de relatório consome 6 horas. No entanto, você deve entregar no mínimo 10 relatórios por semana. Use o Solver para maximizar o número total de tarefas, respeitando o limite de horas e a necessidade mínima de relatórios.
Função objetivo: maximizar o número de tarefas concluídas.
Restrições:
Disponibilidade de 120 horas por semana.
Produzir no mínimo 10 relatórios.










— Comentários 0
, Reações 1
Seja o primeiro a comentar