O que é Modelagem Matemática?
Modelagem matemática é o processo de usar fórmulas e equações para representar situações do mundo real. Ela nos ajuda a prever resultados, entender relações entre variáveis e tomar decisões informadas.
Regressão Logística
A Regressão Logística é uma técnica estatística usada para prever resultados binários (sim/não, 0/1) com base em uma ou mais variáveis independentes. Diferente da regressão linear, que prevê valores contínuos, a regressão logística prevê probabilidades de um evento ocorrer.
A ideia central é modelar a probabilidade de um evento acontecer usando a função logística (também chamada de sigmoide). A função logística mapeia qualquer valor real para um valor entre 0 e 1, que pode ser interpretado como uma probabilidade.
A equação da regressão logística é:
\[ P(Y=1) = \frac{1}{1 + e^{-(aX + b)}} \]
Onde:
- \(P(Y=1)\): Probabilidade de o evento acontecer.
- \(X\): Variável independente (o fator que influencia).
- \(a\): Coeficiente que indica o impacto de \(X\) na probabilidade.
- \(b\): Intercepto.
- \(e\): Número de Euler (aproximadamente 2,71828).
Quando Usar?
- Quando você quer prever um resultado binário (ex.: se um cliente vai comprar ou não, se um paciente tem uma doença ou não).
- Quando a variável dependente é categórica com duas classes (0 ou 1).
Regressão Logística no Excel
No Excel, não há uma função nativa para regressão logística, mas podemos usar o Solver para ajustar o modelo. O Solver é uma ferramenta de otimização que ajusta os coeficientes \(a\) e \(b\) para maximizar a verossimilhança dos dados.
A log-verossimilhança é a melhor forma de avaliar o ajuste do modelo porque mede a probabilidade de observar os dados reais sob os parâmetros do modelo. Diferente do erro quadrático médio, que pode não ser adequado para variáveis binárias, a log-verossimilhança reflete a adequação do modelo considerando distribuições estatísticas apropriadas, como a distribuição Bernoulli na regressão logística.
Passo a Passo no Excel
1. Organize os Dados
- Coloque os dados em colunas. Exemplo:
| Idade (X) | Comprou (Y) |
|---|---|
| 15 | 0 |
| 20 | 1 |
| 25 | 0 |
| 30 | 1 |
| 35 | 1 |
| 40 | 1 |
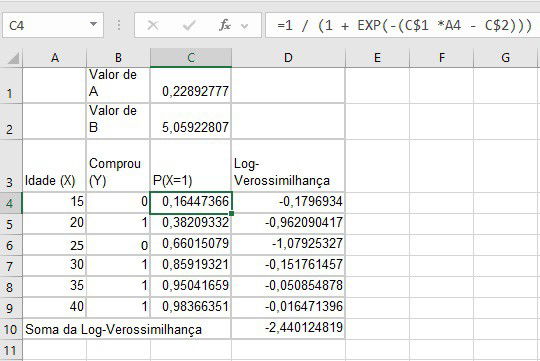
2. Defina a Função Logística
- Em uma coluna, calcule a probabilidade prevista usando a função logística:
\[ P(Y=1) = \frac{1}{1 + e^{-(aX + b)}} \]
- Use valores iniciais para \(a\) e \(b\) (ex.: \(a = 0\), \(b = 0\)).
3. Calcule a Log-Verossimilhança
- A log-verossimilhança é uma medida de quão bem o modelo se ajusta aos dados. Ela é calculada como:
\[ \text{Log-Verossimilhança} = \sum_{i=1}^n \left[ Y_i \cdot \ln(P(Y_i=1)) + (1 - Y_i) \cdot \ln(1 - P(Y_i=1)) \right] \]
- O objetivo é maximizar essa função.
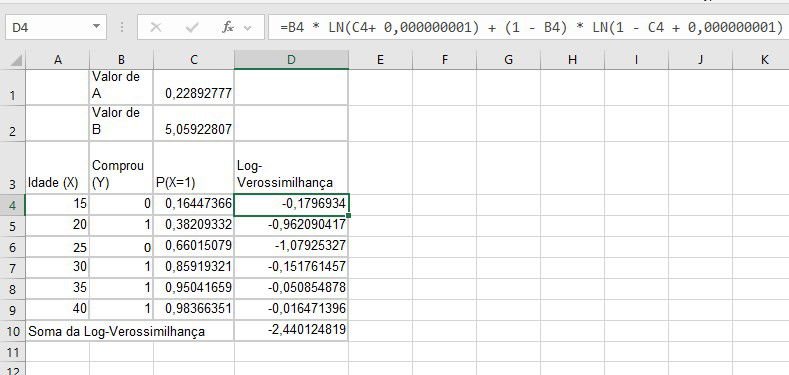
É recomendado somar um valor bem pequeno (0,0000001) dentro do LN para não dar erro na fórmula, afinal, LN(0) é indeterminado.
4. Use o Solver
- Vá para a aba Dados > Solver.
- Defina a célula da log-verossimilhança como Objetivo.
- Defina as células de \(a\) e \(b\) como Variáveis de Decisão.
- Configure o Solver para Maximizar a log-verossimilhança.
- Execute o Solver para ajustar os coeficientes \(a\) e \(b\).
O Solver segue um processo similar ao Monte Carlos, isto é, ele "testa" valores e caminha até encontrar o valor máximo (ou mínimo) mais adequado. É recomendado para processos não lineares utilizar do otimizador GRG Nonlinear (Generalized Reduced Gradient), no caso ao invés de ser 100% aleatório, ele segue um gradiente descendente para encontrar os melhores valores de A e B.
Devido a essa característica do otimizador, lembre-se de sempre começar nos pontos 0 e 0 para A e para B respectivamente. Também lembre-se que se o resultado for um B muito grande, provavelmente indica que a Regressão Logística está perfeita demais com diversas respostas possíveis.
5. Interprete os Resultados
- Os coeficientes \(a\) e \(b\) ajustados pelo Solver são usados para prever probabilidades.
- O coeficiente \(a\) indica o impacto da variável \(X\) na probabilidade do evento.
- O coeficiente \(b\) é o intercepto, que representa a probabilidade quando \(X = 0\).
Exemplo Prático
Dados
| Idade (X) | Comprou (Y) |
|---|---|
| 15 | 0 |
| 20 | 1 |
| 25 | 0 |
| 30 | 1 |
| 35 | 1 |
| 40 | 1 |
Resultados do Solver
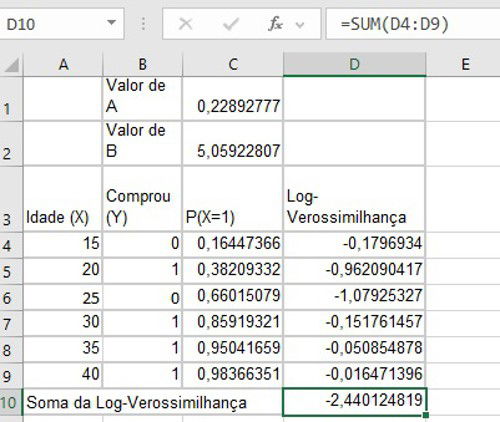
- Coeficiente \(a\): 0,228927774
- Coeficiente \(b\): 5,059228074
Equação da Regressão Logística:
\[ P(Y=1) = \frac{1}{1 + e^{-(0,2 \cdot X - 5)}} \]
Previsão
- Para uma pessoa de 30 anos:
\[ P(Y=1) = \frac{1}{1 + e^{-(0,2 \cdot 30 - 5)}} \approx 0,85 \]
- Há 85% de chance de compra. Logo, por ser acima de 50%, é esperado que irá comprar.
Exercícios
Exercício 1: Compra de Produto
| Idade (X) | Comprou (Y) |
|---|---|
| 25 | 0 |
| 35 | 1 |
| 40 | 0 |
| 45 | 1 |
| 55 | 1 |
a) Qual é a equação da regressão logística?
b) Qual é a probabilidade de uma pessoa de 40 anos comprar o produto?
c) O que o coeficiente \(a\) representa nesse contexto?
Exercício 2: Diagnóstico Médico
| Idade (X) | Doença (Y) |
|---|---|
| 30 | 0 |
| 35 | 0 |
| 40 | 1 |
| 41 | 0 |
| 50 | 1 |
| 60 | 1 |
a) Qual é a equação da regressão logística?
b) Qual é a probabilidade de um paciente de 55 anos ter a doença?
c) O que o coeficiente \(b\) representa nesse contexto?
Exercício 3: Inadimplência
| Renda (X) | Inadimplente (Y) |
|---|---|
| 2000 | 0 |
| 2900 | 1 |
| 3000 | 0 |
| 3500 | 1 |
| 4000 | 1 |
| 5000 | 1 |
a) Qual é a equação da regressão logística?
b) Qual é a probabilidade de um cliente com renda de R$ 3500 ser inadimplente?
c) O que o coeficiente \(a\) representa nesse contexto?











— Comentários 0
, Reações 1
Seja o primeiro a comentar