Introdução
Para quaisquer dois conjuntos de dados que você possa encontrar, existem duas alternativas viáveis de coleta de dados que pode ser feito para descrever a interação entre os dois conjuntos.
A primeira é descrever o quanto as variáveis estão associadas. Utiliza-se para isso a correlação já ensinada, onde o tamanho do coeficiente de correlação indicada o quanto estão associadas.
A segunda é tentar estabelecer uma relação entre as duas variáveis, onde consegue-se dizer o quanto uma variável muda se diminuirmos ou aumentarmos a segunda.
Relação funcional
Como sabemos, o perímetro e o lado de um quadrado estão relacionados. A relação que os liga é perfeitamente definida e pode ser expressa por meio de uma sentença matemática:
\[ 2p = 4l \]
Onde 2p é o perímetro e l é o lado.
Atribuindo-se, então, um valor qualquer a R, é possível determinar exatamente o valor de 2p.
Consideremos, agora, a relação que existe entre o peso e a estatura de um grupo de pessoas. É evidente que essa relação não é do mesmo tipo da anterior; ela é bem menos precisa. Assim, pode acontecer que a estaturas diferentes correspondam pesos iguais ou que a estaturas iguais correspondam pesos diferentes. Contudo, em média, quanto maior a estatura, maior o peso.
As relações do tipo perímetro - lado são conhecidas como relações funcionais e as do tipo peso- estatura, como relações estatísticas. As relações estatísticas podem ser representadas a partir de uma função, também chamada de regressão linear simples.
Objetivos da regressão linear simples
- Predizer valores de uma variável dependente (Y) em função de uma variável independente (X).
- Conhecer o quanto variações de X podem afetar Y.
Regressão Linear Simples
A regressão linear simples é usada para examinar a relação entre uma variável dependente e uma variável independente. Depois de realizar uma análise, as estatísticas de regressão podem ser usadas para prever a variável dependente quando a variável independente é conhecida. A regressão vai além da correlação, adicionando recursos de previsão.
As pessoas usam a regressão em um nível intuitivo todos os dias. Nos negócios, um homem bem vestido é considerado um sucesso financeiro. Uma mãe sabe que mais açúcar na dieta de seus filhos resulta em níveis mais altos de energia. A facilidade de acordar de manhã muitas vezes depende de quão tarde você foi para a cama na noite anterior. A regressão quantitativa adiciona precisão ao desenvolver uma fórmula matemática que pode ser usada para fins preditivos.
Por exemplo, um pesquisador médico pode querer usar o peso corporal (variável independente) para prever a dose mais apropriada para um novo medicamento (variável dependente). O propósito de executar a regressão é encontrar uma fórmula que se encaixe no relacionamento entre as duas variáveis. Em seguida, você pode usar essa fórmula para prever valores para a variável dependente quando apenas a variável independente for conhecida. Um médico pode prescrever a dose adequada com base no peso corporal de uma pessoa.
A linha de regressão (conhecida como a linha de mínimos quadrados) é um gráfico do valor esperado da variável dependente para todos os valores da variável independente. Tecnicamente, é a linha que "minimiza os resíduos quadrados". A linha de regressão é a que melhor se ajusta aos dados em um gráfico de dispersão.
Usando a equação de regressão, a variável dependente pode ser prevista a partir da variável independente. A inclinação da linha de regressão (b) é definida como a subida dividida pela corrida. A intersecção y (a) é o ponto no eixo y onde a linha de regressão interceptaria o eixo y. A inclinação e a intercepção y são incorporadas na equação de regressão. A interceptação é geralmente chamada de constante ou coeficiente linear e a inclinação é chamada de coeficiente angular. Como o modelo de regressão geralmente não é um preditor perfeito, há também um termo de erro na equação.
Na equação de regressão, y é sempre a variável dependente e x é sempre a variável independente. Aqui estão três maneiras equivalentes de descrever matematicamente um modelo de regressão linear:
\[ y = (\text{ângulo} x) + \text{intercepto} + \text{erro} \]
\[ y = (\text{coeficiente angular} · x) + \text{coeficiente linear} + \text{erro} \]
\[ y = a*x + b + e \]
Nós chamamos de regressão linear simples a reta que minima o erro, calculando A e B de forma que o valor esperado do erro seja zero.
Cálculo das constantes A e B
As constantes são calculadas começando por A. Similar à correlação, o confieciente angular também é calculado a partir da covariância. Sua fórmula é a seguinte:
\[ a = \frac{\sigma_{x,y}}{\sigma_{x}^2} \]
O ângulo é a covariância dividida pela variância da variável independente. Nesse caso percebe-se que ao contrário do coeficinente angular, se mantém apenas uma variável no divisor, mantendo ainda a variância da variável dependente no modelo.
Sabendo-se A calcula-se B:
\[ y = a · x + b + e \]
\[E[y] = E[a · x + b + e] \]
\[ E[y] = E[a · x] + E[b] + E[e] \]
\[ \bar{y} = a · \bar{x} + b + 0 \]
\[ b = \bar{y} - a · \bar{x} \]
Alguns livros escrevem a fórmula direta:
\[ a = \frac{N · (\sum{X · Y}) - (\sum{X}) · (\sum{Y})}{N · (\sum{X^{2}}) - (\sum{X})^{2}} \]
\[ b = \frac{(\sum{Y}) - a · (\sum{X})}{N} \]
Com os coeficinete angular e linear podemos finalmente formar uma reta que melhor explica a relação entre duas variáveis:
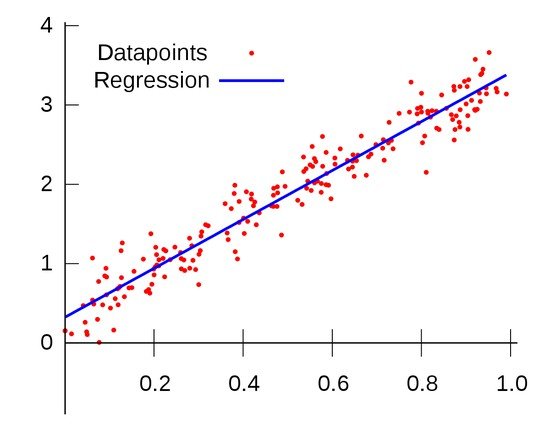
Em uma relação linear, a reta será a que melhor explica essa relação devido à média dos errors ser zero!
Por que dividir a covariância pela variância de \( X \)?
Queremos que \( \beta_1 \) represente "quanto \( Y \) muda, em média, quando \( X \) aumenta 1 unidade".
Mas a covariância sozinha não nos dá isso diretamente, porque:
- Se \( X \) tem uma variância muito grande (valores muito espalhados), a covariância pode ser grande mesmo que a relação entre \( X \) e \( Y \) seja fraca.
- Se \( X \) tem uma variância muito pequena (valores muito concentrados), a covariância pode ser pequena mesmo que a relação seja forte.
Solução: Dividimos a covariância pela variância de \( X \) para normalizar o efeito da escala de \( X \). Isso nos dá uma medida padronizada da relação entre \( X \) e \( Y \).Pense assim:
- Covariância = "Quanto \( X \) e \( Y \) mudam juntos?"
- Variância de \( X \) = "Quanto \( X \) varia sozinho?"
Ao dividir a covariância pela variância de \( X \), estamos calculando:
\[ \beta_1 = \frac{\text{Quanto } X \text{ e } Y \text{ variam juntos}}{\text{Quanto } X \text{ varia sozinho}} \]
Isso responde à pergunta: "Para cada unidade que \( X \) varia, quanto \( Y \) varia, em média?"
Correlação vs Regressão linear
Existem diferenças reais entre correlação e regressão linear, mas, felizmente, elas geralmente não importam. A correlação e a regressão linear fornecem exatamente o mesmo valor de associação (r²) e, para a maioria dos experimentos biológicos, esse é o único resultado realmente importante.
A principal diferença é que a correlação implica em associação entre duas variáveis, mas não em uma interferência direta entre elas, enquanto a regressão linear assume que o aumento da variável independente causa um efeito na variável dependente.
Normalmente muitos vêem a regressão linear como item a ser feito depois de analisada a correlação, onde é possível até visualmente analisar a relação entre duas variáveis. De qualquer forma, é interessante fazer o cálculo das duas por darem resultados diferentes: a correlação diz o quanto a variância é explicada pela relação entre as duas variáveis (29% de correlação implica que só 29% é explicada); enquanto a regressão linear faz um cálculo de relação direta (se aumentarmos 1 de x quanto aumentaremos de y), mas essa relação pode ser falha já que nem toda variação é explicada pela relação entre as duas variáveis.
Os dados sempre serão uma reta?
Uma ótima forma de verificar se a reta é um bom ajuste para seus dados é pelo coeficiente de determinação: r². Ao final o r² é apenas a correlação ao quadrado, por este motivo, considera-se que verificar a regressão linear é muito similar a verificar a correlação entre os dados.
Apesar do coeficiente de correlação dar o mesmo resultado que o coeficiente de determinação numa regressão linear simples, eles são calculados de maneiras diferentes. O coeficiente de determinação é a variação dos dados observados em relação à reta dividido pela variação dos dados:
\[ r² = \frac{\text{Variação dos dados observados em relação à reta}}{\text{Variação total}} \]
Por este motivo, a regressão linear também é conhecida pela regressão dos mínimos quadrados devido à diminuir ao máximo o quadrado dos erros observados.
Exercícios
1) Qual a diferença entre correlação e regressão linear?
2) Faça o gráfico de dispersão e a reta que melhor se ajusta aos dados abaixo:
| Mês (X) | Demanda (Y) |
|---|---|
| 1 | 2400 |
| 2 | 2100 |
| 3 | 2550 |
| 4 | 2700 |
| 5 | 2750 |
| 6 | 2800 |
| 7 | 3000 |
3) No exercício anterior verificou-se que a covariância dos dois conjuntos de dados vale 485,71 e a variância da variável independente (mês) vale 4. Qual o coeficiente angular e linear da reta da regressão linear?
4) Uma loja anotou quantos sungas vendia em 4 dias do ano. Calcule a equação da reta que melhor se ajuste aos seguintes pontos:
| Temperatura (X) | Sungas vendidas (Y) |
|---|---|
| 20 | 10 |
| 25 | 25 |
| 30 | 30 |
| 35 | 40 |
5) No exercício anterior quantas sungas é esperado vender com 40 graus?
6) Sabe-se que quanto mais estudar, maior sua nota. Um aluno duvidando disso resolve verificar o tempo de estudo e a nota de cada aluno em sua classe. Percebeu que a média do tempo de estudo foi de 4 horas e a nota média foi de 7. Percebeu também que a covariância dos dois conjuntos de dados foi de 8 e a variância do tempo de estudo foi de 5. A partir de uma regressão linear, qual a reta que melhor explica a relação entre estudar e sua nota final?
7) No exercício anterior, zezinho teve nota 5,4. Quanto tempo ele estudou pela regressão? Se ele precisava ter nota 8,6 para passar, o quanto ele precisava ter estudado pela regressão?
Gabarito
3) Y = 2128,5713 + 121,4286 · X
4) Y = 1,9 · X - 26
5) 50 sungas
6) Y = 1,6 · X + 0,6
7) Ele estudou 3 horas. Precisava ter estudado 5 horas.
Referências bibliográficas
http://www.biostathandbook.com/linearregression.html
https://www.statpac.com/statistics-calculator/correlation-regression.htm
http://www.kean.edu/~fosborne/bstat/09rc.html
https://edisciplinas.usp.br/pluginfile.php/1479289/mod_resource/content/0/regr_lin.pdf












— Kommentare 0
, Reaktionen 1
Sei der erste der kommentiert