Cálculo de valores a partir de probabilidades
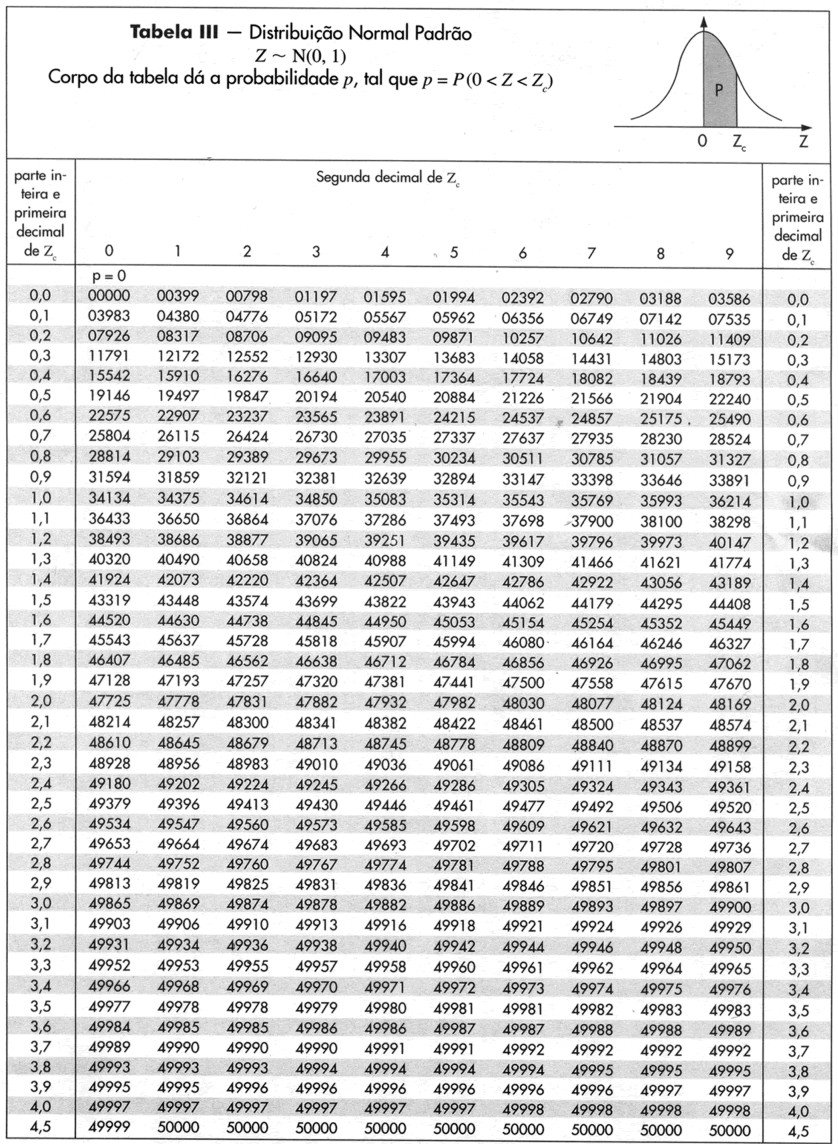
Como dito na aula passada, para descobrirmos as probabilidades de algo normalmente distribuído ocorrer, basta transformar os dados em uma distribuição normal reduzida, onde esta já é estudada pela tabela abaixo:
A transformação é dada pela seguinte fórmula:
\[ z = \frac{x - \bar{x}}{\sigma} \]
Porém, algumas vezes, queremos saber o que acontece com probabilidade X. Para calcular valores a partir de probabilidades, utilizamos os seguintes passos:
- Lembrar que porcentagem ou probabilidades são áreas do gráfico, e não valores de z
- A leitura da tabela é invertida (pela área descobre-se)
- Escolher o lado correto do gráfico (os maiores tempos estão do lado direito)
- Aplicar a variação da fórmula de padronização
A variação da fórmula de padronização consiste:
\[ z = \frac{x - \bar{x}}{\sigma} \]
\[ z*\sigma = x - \bar{x} \]
\[ x = \bar{x} + z · \sigma \]
Em outras palavras, desvio padrão e a média, pode-se calcular qualquer valor para uma dada probabilidade, já que por esta descobre-se Z.
Exemplos
Considera-se uma fábrica que os trabalhadores levam em média 75 minutos para completar uma tarefa com 6 minutos de desvio padrão. Quanto tempo separa os 10% mais rápidos dos 10% mais lentos?
Os 10% mais rápidos estão na parte esquerda do gráfico, se analisarmos, o Z dos 10% mais lento tem valor: -1,28
Os 10% mais lentos estão na parte direita do gráfico, se analisarmos, o z dos 10% mais rápidos tem valor: 1,28
Assim, calcule-se o tempo dos 10% mais rápidos:
\[ x = \bar{x} + z · \sigma \]
\[ x = 75 - 1,28*6 = 67.32 \]
E dos 10% mais lentos:
\[ x = \bar{x} + z · \sigma \]
\[ x = 75 + 1,28*6 = 82.68 \]
A diferença entre o tempo dos dois é:
\[ \text{diferença } = 82.68 - 67.32 = 15.36 \]
Considera-se uma fábrica que os trabalhadores levam em média 75 minutos para completar uma tarefa com 6 minutos de desvio padrão. Quanto tempo leva no mínimo os 5% mais rápidos?
Os 5% mais lentos estão na parte direita do gráfico, se analisarmos, o z dos 5% mais rápidos tem valor: 1,65
Assim, calcule-se o tempo mínimo dos 5% mais rápido:
\[ x = \bar{x} + z · \sigma \]
\[ x = 75 + 1,65 · 6 = 84.9 \]
Simetria na distribuição
Já foi discutido que a distribuição normal é simétrica. Muitas vezes é explorada essa característica:
- Mais ricos ou mais pobres
- Mais rápidos ou mais lentos
- Mais altos ou mais baixo
Fica um alerta: em exercícios em que há uma dualidade, lembre-se que cada dualidade representa 50% da distribuição.
Exemplos
Considera-se uma fábrica que os trabalhadores levam em média 75 minutos para completar uma tarefa com 6 minutos de desvio padrão. Qual o tempo que separa os 10% entre os mais rápidos dos 10% entre os mais lentos?
Neste caso, 10% entre os mais rápidos, que são 50% da distribuição, significa 5% da distribuição na parte direita. Enquanto, 10% entre os mais lentos, que são 50% da distribuição, significa 5% da distribuição na parte esquerda.
O z dos 5% mais rápidos tem valor: 1,65
\[ x = \bar{x} + z · \sigma \]
\[ x = 75 + 1,65 · 6 = 84.9 \]
O z dos 5% mais lentos tem valor: -1,65
\[ x = \bar{x} + z · \sigma \]
\[ x = 75 - 1,65 · 6 = 65.1 \]
A diferença:
\[ \text{diferença } = 84.9 - 65.1 = 19.8 \]
Exercícios
1) Suponha que o tempo necessário para atendimento de clientes em uma central de atendimento telefônico siga uma distribuição normal de média de 8 minutos e desvio padrão de 2 minutos. 25% das chamadas telefônicas requerem pelo menos quanto tempo de atendimento?
2) Suponha que o tempo necessário para atendimento de clientes em uma central de atendimento telefônico siga uma distribuição normal de média de 8 minutos e desvio padrão de 2 minutos. 75% das chamadas telefônicas requerem pelo menos quanto tempo de atendimento?
3) Suponha que o tempo necessário para atendimento de clientes em uma central de atendimento telefônico siga uma distribuição normal de média de 8 minutos e desvio padrão de 2 minutos. Qual é a probabilidade de que um atendimento dure menos de 5 minutos? E mais do que 9,5 minutos? E entre 7 e 10 minutos?
4) A distribuição dos pesos de coelhos criados numa granja pode muito bem ser representada por uma distribuição Normal, com média 5 kg e desvio padrão 0,9 kg. Um abatedouro comprará 5000 coelhos e pretende classificá-los de acordo com o peso do seguinte modo: 15% dos mais leves como pequenos, os 50% seguintes como médios, os 20% seguintes como grandes e os 15% mais pesados como extras. Quais os limites de peso para cada classificação?
5) Uma enchedora automática de refrigerantes está regulada para que o volume médio de líquido em cada garrafa seja de 1000 cm³ e desvio padrão de 10 cm³. Admita que o volume siga uma distribuição normal. Qual é a porcentagem de garrafas em que o volume de líquido é menor que 990 cm³? Qual é a porcentagem de garrafas em que o volume de líquido não se desvia da média em mais do que dois desvios padrões?
6) Uma empresa produz televisores de 2 tipos, tipo A (comum) e tipo B (luxo), e garante a restituição da quantia paga se qualquer televisor apresentar defeito grave no prazo de seis meses. O tempo para ocorrência de algum defeito grave nos televisores tem distribuição normal sendo que, no tipo A, com média de 10 meses e desvio padrão de 2 meses e no tipo B, com média de 11 meses e desvio padrão de 3 meses. Os televisores de tipo A e B são produzidos com lucro de R\$1200 e R\$2100. respectivamente e, caso haja restituição, com prejuízo de R\$2500 e R\$ 7000 respectivamente. Calcule as probabilidades de haver restituição nos televisores do tipo A e do tipo B e seus lucros médios.
7) Uma fábrica de carros sabe que os motores de sua fabricação têm duração normal com média 150000 km e desvio-padrão de 5000 km. Qual a probabilidade de que um carro, escolhido ao acaso, dos fabricados por essa firma, tenha um motor que dure: menos de 170000 km? Entre 140000 km e 165000 km? Se a fábrica substitui o motor que apresenta duração inferior à garantia, qual deve ser esta garantia para que a porcentagem de motores substituídos seja inferior a 0,2%?
8) A média dos diâmetros internos de uma amostra de 200 arruelas produzidas por uma certa máquina é 0,502 cm e o desvio-padrão é 0,005. A finalidade para qual essas arruelas são fabricadas permite a tolerância máxima, para o diâmetro, de 0,496 a 0,508 cm. Se isso não se verificar, as arruelas serão consideradas defeituosas. Determinar a percentagem de arruelas defeituosas produzidas pela máquina, admitindo-se que os diâmetros são distribuídos normalmente.
9) Suponha que as medidas da corrente elétrica em pedaço de fio sigam a distribuição Normal, com uma média de 10 miliamperes e uma variância de 4 miliamperes. Qual a probabilidade de a medida exceder 13 miliamperes? Qual a probabilidade de a medida da corrente estar entre 9 e 11 miliamperes?
10) Suponha que as medidas da corrente elétrica em pedaço de fio sigam a distribuição Normal, com uma média de 10 miliamperes e uma variância de 4 miliamperes. Determine o valor para o qual a probabilidade de uma medida da corrente estar abaixo desse valor seja 98%.
11) O diâmetro do eixo principal de um disco rígido segue a distribuição Normal com média 25,08 cm e desvio padrão 0,05 cm. Se as especificações para esse eixo são 25,00 ± 0,15 cm, determine o percentual de unidades produzidas em conformidades com as especificações.
12) A concentração de um poluente em água liberada por uma fábrica tem distribuição N(8; 1,5). Média 8 e variância 1,5. Qual a chance, de que num dado dia, a concentração do poluente exceda o limite regulatório de 10 ppm?
Gabarito
1) 6,7 minutos
2) 9,34 minutos
3) 6,68%; 22,66%; 53,28%;
4) pequeno < 4,1kg < médio < 5,4 kg < grande < 5,9 kg < extra
5) 15,9%; 95%;
6) Tipo A -> 2,28% e lucro médio de R\$1115,64; Tipo B -> 4,75% e lucro médio de R\$1667,75
7) 99,993%; 97,59%; garantia de 135650 km.
8) 23%;
9) 6,68%; 38,29%;
10) 14,1 miliamperes;
11) 91,92%
12) 5,2%












— Kommentare 0
, Reaktionen 1
Sei der erste der kommentiert