Introdução
Similar à covariância: quando duas variáveis estão ligadas por uma relação estatística, dizemos que existe correlação entre elas.
Relação funcional
Como sabemos, o perímetro e o lado de um quadrado estão relacionados. A relação que os liga é perfeitamente definida e pode ser expressa por meio de uma sentença matemática:
\[ 2p = 4l \]
Onde 2p é o perímetro e l é o lado.
Atribuindo-se, então, um valor qualquer a R, é possível determinar exatamente o valor de 2p.
Consideremos, agora, a relação que existe entre o peso e a estatura de um grupo de pessoas. É evidente que essa relação não é do mesmo tipo da anterior; ela é bem menos precisa. Assim, pode acontecer que a estaturas diferentes correspondam pesos iguais ou que a estaturas iguais correspondam pesos diferentes. Contudo, em média, quanto maior a estatura, maior o peso.
As relações do tipo perímetro - lado são conhecidas como relações funcionais e as do tipo peso- estatura, como relações estatísticas.
Diagrama de dispersão
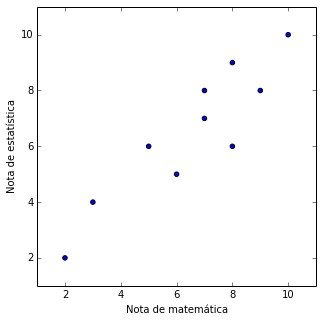
Consideremos uma amostra aleatória, formada por dez dos 98 alunos de uma classe da faculdade A e pelas notas obtidas por eles em Matemática e Estatística:
| Nota de matemática | Nota de estatística |
|---|---|
| 5,0 | 6,0 |
| 8,0 | 9,0 |
| 7,0 | 8,0 |
| 10,0 | 10,0 |
| 6,0 | 5,0 |
| 7,0 | 7,0 |
| 9,0 | 8,0 |
| 3,0 | 4,0 |
| 8,0 | 6,0 |
| 2,0 | 2,0 |
Representando, em um sistema coordenado cartesiano ortogonal, os pares ordenados (xi, y), obtemos uma nuvem de pontos que denominamos diagram a de dispersão. Esse diagrama nos fornece uma ideia grosseira, porém útil, da correlação existente que para este caso existe e é positiva.
O que é Correlação linear
Como a correlação em estudo tem como "imagem" uma reta ascendente, ela é chamada correlação linear positiva.
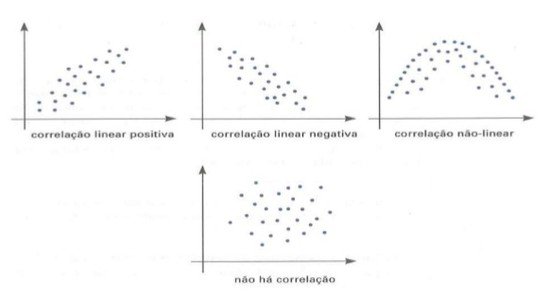
Assim, uma correlação é:
- linear positiva se os pontos do diagrama têm como "imagem" uma reta ascendente;
- linear negativa se os pontos têm como "imagem" uma reta descendente;
- não linear se os pontos têm como "imagem" uma curva.
Se os pontos apresentam-se dispersos, não oferecendo uma "imagem" definida, concluímos que não há relação alguma entre as variáveis em estudo.
Temos, então:
Como calcular o coeficiente de correlação linear
O instrumento empregado para a medida da correlação linear é o coeficiente de correlação. Esse coeficiente deve indicar o grau de intensidade da correlação entre duas variáveis e, ainda, o sentido dessa correlação (positivo ou negativo).
Faremos uso do coeficiente de correlação de Pearson, que é dado por:
\[ r = \dfrac{\sigma_{x,y}}{\sigma_x · \sigma_y} \]
> O coficiente de correlação é a covariância dividida pelo desvio padrão de cada variável estudada
Outra fórmula seria:
\[ r = \frac{\sum{(x - \bar{x})(y - \bar{y})}}{\sqrt{\sum{(x - \bar{x})^{2}}} · \sqrt{\sum{(y - \bar{y})^{2}}}} \]
Diferente da covariância, onde só podíamos analisar se é positiva ou negativa, o coeficiente de correlação nos garante muito mais informação por ele estar entre -1 e 1, em outras palavras, pertence ao intervalo [-1, +1].
Assim:
a. se a correlação entre duas variáveis é perfeita e positiva, então r = +1 ;
b. se a correlação é perfeita e negativa, então r = -1;
c. se não há correlação entre as variáveis, então r = O.
Para:
| valor de r (+ ou -) | interpretação |
|---|---|
| 0 a 19% | Correlação muito fraca |
| 20% a 39% | Correlação fraca |
| 40% a 59% | Correlação moderada |
| 60% a 79% | Correlação forte |
| 80% a 100% | Correlação muito forte |
Propriedades da correlação
1. O coeficiente de correlação independe das unidades de medida das variáveis; é um número adimensional que varia entre –1 e +1, isto é, -1 ≤ r ≤ + 1.
2. O coeficiente de correlação de uma variável e ela mesma é igual a +1.
3. A permutação das variáveis não altera o resultado do coeficiente de correlação, isto é, rXY = rYX.
4. Somando-se ou subtraindo-se uma constante a uma ou a ambas as variáveis, o coeficiente de correlação não se altera.
5. Multiplicando-se ou dividindo-se uma ou ambas as variáveis por uma constante, o coeficiente de correlação não se altera.
Exemplos
Complete o esquema de cálculo do coeficiente de correlação para os valores das variáveis x e y:
| x | y |
|---|---|
| 12 | 4 |
| 10 | 6 |
| 8 | 8 |
| 12 | 10 |
| 14 | 12 |
A covariância do conjunto de dados é 2,4. Enquanto o desvio padrão da primeira vale 2,04 e da segunda 2,83.
Logo:
\[ r = \frac{2,4}{2,04·2,83} = 0,41 = 41\% = \text{correlação moderada} \]
Exercícios
1) Desenhe os diferentes diagramas de dispersão que podem ser encontrados para as seguintes correlações: correlação positiva perfeita, correlação negativa e correlação não-linear.
2) Faça o diagrama de dispersão das seguintes variáveis:
| x | y |
|---|---|
| 50 | 10 |
| 60 | 20 |
| 80 | 100 |
| 50 | 25 |
Qual tipo de correlação essas variáveis apresentam?
3) Qual o coeficiente de correlação das variáveis do exercício anterior?
4) Qual o coeficiente de correlação das seguintes variáveis:
| x | y |
|---|---|
| 10 | 20 |
| 30 | 5 |
| 15 | 15 |
| 5 | 50 |
5) Qual o coeficiente de correlação das seguintes variáveis:
| x | y |
|---|---|
| 10 | 1 |
| 30 | 2 |
| 15 | 40 |
| 5 | 3 |
6) Davi analisou que a covariância de dois conjuntos de dados era igual a 10, e o desvio padrão de um conjunto tem valor 2 e de outro tem valor 5. Qual o coeficiente de correlação dos dois conjuntos de dados?
7) Mais uma vez, Davi analisou que a covariância de dois conjuntos de dados era igual a 200, e o desvio padrão de um conjunto tem valor 20 e de outro tem valor 40. Mas, depois de já ter feito essa análise, teve que modificar um dos conjuntos de dados, dividindo ele por 10.000. Qual o coeficiente de correlação dos dois conjuntos de dados agora?
Gabarito
2) Correlação linear positiva
3) 94%
4) -83%
5) 0%
6) 100%
7) 25%












— Kommentare 0
, Reaktionen 1
Sei der erste der kommentiert