Formas de distribuição de frequência
As variáveis podem ser observadas e estudadas muito mais facilmente quando dispusermos valores ordenados em uma coluna e colocarmos, ao lado de cada valor, o número de vezes que aparece repetido.
Frequência Simples
Denominamos frequência o número de repetições de determinado valor da variável estudada. A distribuição de frequência é a análise de todas essas frequências e como elas estão distribuídas.
Como exemplo, vamos analisar uma table de distribuição de frequência de alturas de estudantes de uma determinada turma:
| Altura (cm) | Frequência |
|---|---|
| 151 | 1 |
| 152 | 0 |
| 153 | 2 |
| 154 | 1 |
| 155 | 4 |
| 156 | 3 |
| 157 | 1 |
| 158 | 2 |
| 159 | 0 |
| 160 | 5 |
| 161 | 4 |
| 162 | 3 |
| 163 | 2 |
| 164 | 3 |
| 165 | 1 |
| 166 | 1 |
Frequência por Classes
Mas o processo dado ainda é inconveniente, já que exige muito espaço, mesmo quando o número de valores da variável (n) é de tamanho razoável. Sendo possível, a solução mais aceitável, pela própria natureza da variável contínua, é o agrupamento dos valores em vários intervalos. Como exemplo:
| Altura (cm) | Frequência |
|---|---|
| 150 - 155 | 8 |
| 155 - 160 | 11 |
| 160 - 165 | 13 |
| 165 - 170 | 1 |
Os intervalos criados são chamados de classes. Na tabela acima, à direita, podemos ver a frequência de cada classe.
> Classes de frequência ou apenas classes são intervalos de uma variação da variável.
Nomenclaturas em frequências
Extremos
> Denominamos também de limites de classe os extremos de cada classe
No caso há o limite inferior e o superior de cada classe. Nos exemplos anteriores, os limites inferiores seriam: 150, 155, 160, 165; e os superiores: 155, 160, 165, 170.
Amplitude
> Amplitude de um intervalo de classe ou apenas amplitude é a medida do intervalo que define a classe.
Ela é obtida pela diferença entre os limites superiores e inferiores. Nos exemplos anteriores, há as seguintes amplitudes para cada classe em ordem: 5.
\[ \text{amplitude: } 155 - 150 = 160 - 155 = 165 - 160 = 170 - 165 = 5 \]
Amplitude total da distribuição
> Amplitude total da distribuição é a diferença entre o limite superior da última classe e o limite inferior da primeira classe. Ou também a diferença entre o menor dado e o maior.
No exemplo, a amplitude total seria 20, por o limite inferior da primeira classe ser 150 e o limite superior da última classe ser 170.
Número de classes
A primeira preocupação que temos em uma distribuição de frequência é a determinação do número de classes.
Normalmente é utilizado a regra de Sturges, que nos dá o número de classes a partir da seguinte função:
\[ \text{quantidade de classes = } 1 + 3,3 * log(n) \]
A amplitude de cada classe é dada pela divisão entre a amplitude total e o número de classes:
\[ \text{amplitude de cada classe = } \frac{\text{amplitude total}}{\text{número de classes}} \]
Tipos de frequência
Frequência simples ou absoluta
> Frequência simples ou absoluta são os valores que realmente representam o número de dados de cada classe
Exemplo:
| Altura (cm) | Frequência simples |
|---|---|
| 150 - 155 | 8 |
| 155 - 160 | 11 |
| 160 - 165 | 13 |
| 165 - 170 | 1 |
Frequência relativa
> Frequência relativa são os valores das razões entre as frequências simples e a frequência total
Exemplo com total 33:
| Altura (cm) | Frequência relativa |
|---|---|
| 150 - 155 | 8/33 |
| 155 - 160 | 11/33 |
| 160 - 165 | 13/33 |
| 165 - 170 | 1/33 |
Frequência acumulada
> Frequência acumulada é o total das frequências de todos os valores inferiores ao limite superior do intervalo de uma dada classe.
| Altura (cm) | Frequência acumulada |
|---|---|
| 150 - 155 | 8 |
| 155 - 160 | 19 |
| 160 - 165 | 32 |
| 165 - 170 | 33 |
Frequência acumulada relativa
> Frequência acumulada relativa é a frequência acumulada das classes dividido pelo total da distribuição.
Exemplo com total 33:
| Altura (cm) | Frequência acumulada relativa |
|---|---|
| 151 - 155 | 8/33 |
| 156 - 160 | 19/33 |
| 161 - 165 | 32/33 |
| 166 - 170 | 33/33 |
Representação gráfica
Além do gráfico de barras ou histograma para representar graficamente uma distribuição de frequência podemos utilizar as seguintes possibilidades.
Polígono de frequência
Para uma representação gráfica da distribuição de frequência se utiliza o polígono de frequência.
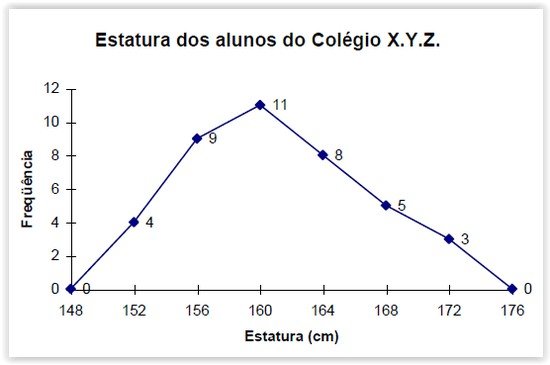
> O polígono de frequência é um gráfico em linha, sendo as frequências marcadas sobre perpendiculares ao eixo horizontal, levantadas pelos pontos médios dos intervalos de classe.
Exemplo:
Polígono de frequência acumulada
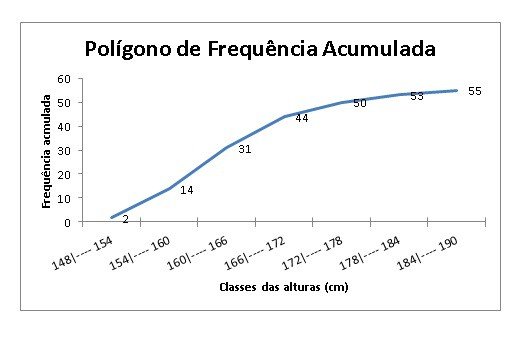
> O polígono de frequência acumulada é traçado marcando-se as frequências acumuladas sobre perpendiculares ao eixo horizontal, levantadas aos pontos correspondentes aos limites superiores dos intervalos de classe.
Exemplo:
As formas das curvas de frequência
Curvas em forma de um sino
> Caracterizam-se pelo fato de apresentarem um valor máximo na região central. São as mais encontradas na natureza. Exemplos: alturas, notas de alunos, crescimento diário de preços de ações etc...
Podem ser simétricas:
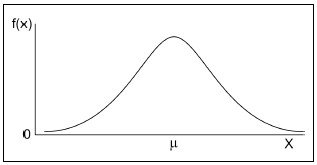
E podem ser assimétricas:
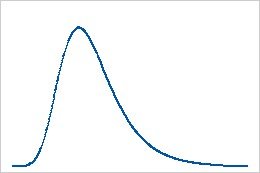
As assimétricas podem ser enviesadas para direita ou esquerda, ou respectivamente assimétricas positivas ou negativas.
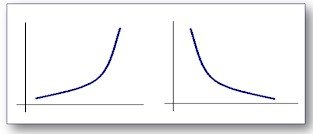
Curvas em forma de jota
> São relativas às distribuições extremamente assimétricas. Normalmente encontradas em funções exponenciais. Exemplos: crescimento populacional, valor de um fundo, preço de produtos no tempo.
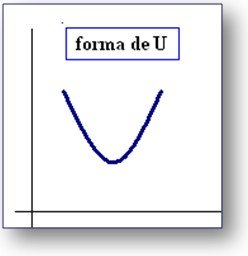
Curvas em forma de U
> São relativas às distribuições que apresentam ordenadas máximas em ambas as extremidades. Pode ser encontrada em situações bem específicas: temperatura durante o ano, taxa de mortalidade por idade.
Transformações na tabela de frequência
Curva polida: quando a curva da amostra não sai bem como imaginávamos
Se você plotar um histograma das alturas de 100 pessoas, ele pode ter picos e vales irregulares. Fazer a curva polida (ou suavizada) após coletar as frequências de uma amostra é uma técnica comum em estatística e análise de dados, principalmente quando se trabalha com histogramas ou distribuições empíricas. Essa suavização é feita por vários motivos importantes:
- Redução de Ruído e Flutuações Aleatórias
- Melhor Visualização da Distribuição Real
- Facilitar Comparações e Interpretações
- Estimar Probabilidades de Forma Contínua
As técnicas mais comuns de suavização são: Kernel Density Estimation (KDE), Médias Móveis ou Splines (Regressão Não-Paramétrica). Vamos entender aqui o método mais simples para fazer a curva polida. A média móvel simples (Simple Moving Average - SMA) de ordem n n é calculada como:
\[ SMA_t = \frac{x_t + x_{t-1} + x_{t-2} + \dots + x_{t-n+1}}{n} \]
Onde:
- \( x_t \) = valor no tempo \( t \)
- \( n \) = número de períodos considerados
Suponha que coletamos as seguintes frequências diárias de acessos a um site durante 10 dias:
| Dia (\( t \)) | Acessos (\( x_t \)) |
|---|---|
| 1 | 120 |
| 2 | 150 |
| 3 | 130 |
| 4 | 170 |
| 5 | 160 |
| 6 | 140 |
| 7 | 190 |
| 8 | 180 |
| 9 | 170 |
| 10 | 200 |
Aplicamos a fórmula para os dias a partir do 3º:
- Dia 3:
\[ SMA_3 = \frac{130 + 150 + 120}{3} = \frac{400}{3} \approx 133,3 \]
- Dia 4:
\[ SMA_4 = \frac{170 + 130 + 150}{3} = \frac{450}{3} = 150 \]
- Dia 5:
\[ SMA_5 = \frac{160 + 170 + 130}{3} = \frac{460}{3} \approx 153,3 \]
... e assim por diante até o Dia 10.
| Dia (\( t \)) | Acessos (\( x_t \)) | SMA(3) (Curva Polida) |
|---|---|---|
| 1 | 120 | - |
| 2 | 150 | - |
| 3 | 130 | 133,3 |
| 4 | 170 | 150,0 |
| 5 | 160 | 153,3 |
| 6 | 140 | 156,7 |
| 7 | 190 | 163,3 |
| 8 | 180 | 170,0 |
| 9 | 170 | 180,0 |
| 10 | 200 | 183,3 |
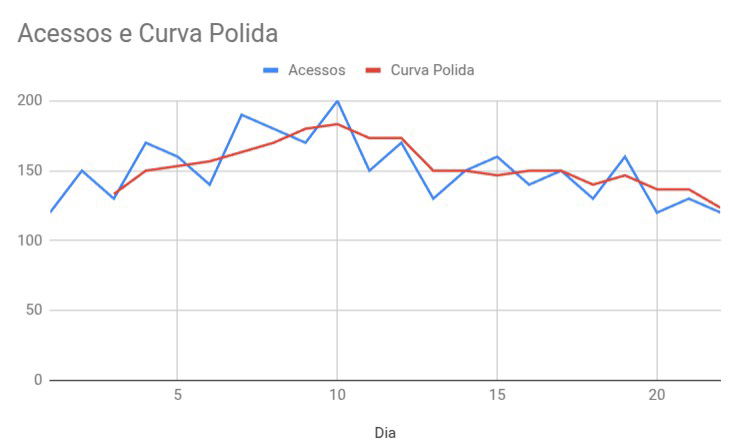
Veja o resultado final como a curva polida não possue os "saltos" repentinos da distribuição amostral inicial, suavizando sua curva.
Outras transformações
Além da curva polida (suavização), existem várias transformações matemáticas aplicadas a dados para melhorar sua distribuição, linearidade ou interpretação. Abaixo está um resumo das principais:
| Transformação | Fórmula | Quando Usar | Exemplo de Aplicação |
|---|---|---|---|
| Logarítmica | \( \log(x) \) ou \( \ln(x) \) | Dados com assimetria positiva (cauda longa à direita). | Renda, tamanho de cidades, preços de ações. |
| Raiz Quadrada | \( \sqrt{x} \) | Dados de contagem (Poisson) ou assimetria moderada. | Número de cliques, acidentes por dia. |
| Inversa | \( \frac{1}{x} \) | Relações inversas (ex.: tempo vs. velocidade). | Tempo entre eventos, taxas de falha. |
| Box-Cox | \( \frac{x^\lambda - 1}{\lambda} \) | Normalização de dados não-lineares (ajusta \( \lambda \) automaticamente). | Dados com variância não constante. |
| Padronização (Z-score) | \( \frac{x - \mu}{\sigma} \) | Quando precisa de escala comparável (média=0, dp=1). | Machine Learning, algoritmos sensíveis a escala. |
| Normalização Min-Max | \( \frac{x - \min(X)}{\max(X) - \min(X)} \) | Dados em intervalos fixos (ex.: [0, 1]). | Redes neurais, imagens (pixels). |
Exercícios
1) As notas obtidas por 50 alunos de uma classe foram:
1 2 3 4 5 6 6 7 7 8
2 3 3 4 5 6 6 7 8 8
2 3 4 4 5 6 6 7 8 9
2 3 4 5 5 6 6 7 8 9
2 3 4 5 5 6 7 7 8 9
Decidiu-se dividir as frequências em 5 classes (0-2, 2-4, 4-6, 6-8 e 8-10). Responda:
a) Complete a distribuição de frequência das classes.
b) Qual a amplitude amostral?
c) Qual a amplitude da distribuição?
d) Qual o número de classes da distribuição?
e) Qual o limite superior da quarta classe?
f) Qual o limite superior da classe de ordem 2?
g) Qual a amplitude do segundo intervalo de classe?
2) Conhecida as notas de 50 alunos:
84 68 33 52 47 73 68 61 73 77
74 71 81 91 65 55 57 35 85 88
59 80 41 50 53 65 76 85 73 60
67 41 78 56 94 35 45 55 64 74
65 94 66 48 39 69 89 98 42 54
Obtenha a distribuição de frequência, tendo 30 para limite inferior da primeira classe e 10 para intervalo de classe.
3) Os resultados do lançamento de um dado 50 vezes foram os seguintes:
1 1 1 1 1 1 1 2 2 1
2 2 2 2 2 3 3 3 3 3
4 4 4 4 4 4 4 4 4 4
5 5 5 3 3 3 5 5 5 5
5 5 6 6 6 6 6 6 6 6
Forme uma distribuição de frequência sem intervalos de classe.
4) Dada a distribuição de frequência:
| x | Frequência 1 | Frequência 2 |
|---|---|---|
| 3 | 2 | 2 |
| 4 | 5 | 5 |
| 5 | 12 | 9 |
| 6 | 10 | 6 |
| 7 | 8 | 2 |
| 8 | 3 | 1 |
Determine:
a) O somatório das frequências
b) As frequências relativas
c) As frequências acumuladas
d) As frequências relativas acumuladas
5) Confeccione a curva polida relativa à distribuição de frequência:
| i | classes | Frequência |
|---|---|---|
| 1 | 4 - 8 | 2 |
| 2 | 8 - 12 | 5 |
| 3 | 12 - 16 | 9 |
| 4 | 16 - 20 | 6 |
| 5 | 20 - 24 | 2 |
| 6 | 24 - 28 | 1 |
6) Cite o tipo de curva correspondente a cada distribuição a seguir:
a) Número de mulheres de 15 a 30 anos, em uma dada população, casadas, classificadas segundo o número de vezes que hajam contraído matrimônio;
b) Notas de alunos que cursam a última série do 2º grau, em uma dada população;
c) Coeficiente de mortalidade por acidente, por grupo de idade;
d) Tempo de estacionamento de veículos motorizados em uma área de congestionamento;
e) Número de homens capacitados, por grupo de idade, que estão desempregados.
7) Os números abaixo apresentam os coeficientes de liquidez obtidos da análise do balanço de 50 indústrias:
3,9 7,4 10,0 11,8 2,3 4,5 10,5 8,4 15,6 7,6
18,8 2,9 2,3 0,4 5,0 9,0 5,5 9,2 12,4 8,7
4,5 4,4 10,6 5,6 8,5 2,4 17,8 11,6 0,8 4,4
7,1 3,2 2,7 16,2 2,7 9,5 13,1 3,8 6,3 7,9
4,8 5,3 12,9 6,9 6,3 7,5 2,6 3,3 4,6 16,0
a) Forme com esses dados uma distribuição com intervalos de classe iguais a 3, tais que os limites inferiores sejam múltiplos de 3;
b) Confeccione o histograma correspondente.
8) Um grau de nebulosidade, registrado em décimos, ocorre de acordo com a distribuição abaixo:
| Nebulosidade | Frequência |
|---|---|
| 0 - 0,5 | 320 |
| 0,5 - 1,5 | 125 |
| 1,5 - 2,5 | 75 |
| 2,5 - 3,5 | 65 |
| 3,5 - 4,5 | 45 |
| 4,5 - 5,5 | 45 |
| 5,5 - 6,5 | 55 |
| 6,5 - 7,5 | 65 |
| 7,5 - 8,5 | 90 |
| 8,5 - 9,5 | 145 |
| 9,5 - 10 | 676 |
Construa o histograma correspondente.
9) Considerando a distribuição abaixo:
| Classes | Frequência |
|---|---|
| 1 - 2 | 7 |
| 2 - 3 | 3 |
| 3 - 4 | 10 |
| 4 - 5 | 11 |
| 5 - 6 | 12 |
| 6 - 7 | 37 |
| 7 - 8 | 35 |
| 8 - 9 | 45 |
| 9 - 10 | 39 |
| 10 - 11 | 30 |
| 11 - 12 | 25 |
Construa o histograma correspondente.
10) A tabela abaixo apresenta uma distribuição de frequência das áreas de 400 lotes:
| Áreas (m²) | Número de lotes |
|---|---|
| 300 - 400 | 14 |
| 400 - 500 | 46 |
| 500 - 600 | 58 |
| 600 - 700 | 76 |
| 700 - 800 | 68 |
| 800 - 900 | 62 |
| 900 - 1000 | 48 |
| 1000 - 1100 | 22 |
| 1100 - 1200 | 6 |
Com referência a essa tabela, determine:
a) a amplitude total;
b) o limite superior da quinta classe;
c) o limite inferior da oitava classe;
d) o ponto médio da sétima classe;
e) amplitude do intervalo da segunda classe;
f) frequência da quarta classe;
g) frequência relativa da sexta classe;
h) frequência acumulada da quinta classe;
i) o número de lotes cuja área não atinge 700 m²;
j) O número de lotes cuja área atinge e ultrapassa 800 m²;
l) A percentagem dos lotes cuja área seja maior ou igual a 900 m²;
m) A percentagem dos lotes cuja área é de 500 m², no mínimo, mas inferior a 1000 m²;












— Kommentare 0
, Reaktionen 1
Sei der erste der kommentiert