O curso Informática Avançada 2 presume que o aluno tenha lido e entendido o curso de Informática Avançada 1. No curso 1, vimos como aplicativos de planilhas, tomando o excel de exemplo, funcionam: seu layout, como escrever, como fazer conta e suas funções.
Um leve resumo
- Em aplicativos planilha como o Excel escrevemos as fórmulas em uma célula;
- Na célula, para escrever uma função ou uma soma matemática, você deve começar com "=";
- Dentro das células, depois de um sinal de igual, puro texto deve ser escrito entre aspas;
- Caso queira construir uma função, você deve escrever o nome da função e logo depois: abrir parêntesis, escrever os argumentos da função (inputs) separados por ";" e fechar parêntesis.
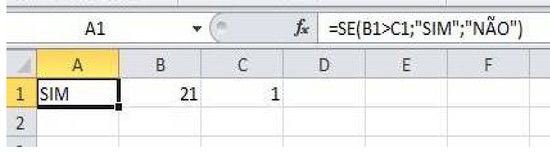
Repare no exemplo acima, primeiro foi escrito o sinal de igual ("="), logo depois foi escrita a função SE. A função SE toma 3 argumentos: uma afirmação que pode ser verdadeira ou falsa; o que acontece se for verdadeira; o que acontece se for falsa. No exemplo, a afirmação é "B1 > C1" e irá retornar "SIM" caso verdadeira e "NÃO" caso falsa. B1 é 21 e C1 é 1, logo 21 > 1, o que torna a afirmação verdadeira, retornando "SIM".
Vamos aprender mais funções então?
A função E
A função E é utilizada para testar se os argumentos envolvidos são ou não verdadeiros. O resultado desta função retornará verdadeiro somente se todos os argumentos que compõem a função são verdadeiros, basta que um argumento seja falso para que ela retorne falso.
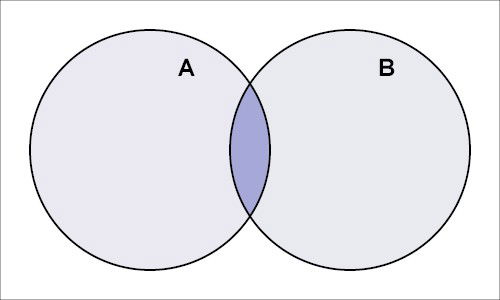
Na matemática a função E seria a interseção entre dois grupos. No caso, só os valores que pertencem aos dois grupos fazem parte da interseção.
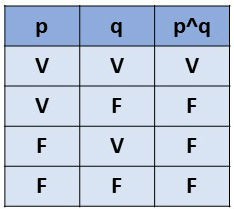
Também vemos essa função aparecendo em "tabelas verdade" quando estudamos lógica matemática, principalmente para concurso público.
No Excel:
=E(argumento 1; argumento 2; argumento 3; ...)
Argumento no caso é um teste lógico, por exemplo: "A5 = 10" ou "A6 > 18".
Exercício
Identificar as pessoas que são solteiras e tenham 22 anos ou mais e casadas e maiores de 21 anos.
| Nome | Estado Civil | Idade |
|---|---|---|
| Caio Mansera | Casado(a) | 36 |
| Raul Guedes | Solteiro (a) | 22 |
| Antônia Orsolato | Casado(a) | 25 |
| Quênia Rhuby | Casado(a) | 26 |
| Fábio Souza | Solteiro (a) | 28 |
| Danielle Farrine | Solteiro (a) | 21 |
| Edivaldo Chopp | Solteiro (a) | 43 |
| Césas Alfeir | Casado(a) | 22 |
| Paschoal Ranieri | Solteiro (a) | 26 |
Solução
=E(B2="Solteiro(a)";C2>=22)
=E(B2="Casado(a)";C2>21)
A função OU
Assim como a função E, a função OU também é utilizada para testar se os argumentos envolvidos são ou não verdadeiros. O resultado desta função retornará verdadeiro se ao menos um dos argumentos que compõem a função é verdadeiro. Todos os argumentos devem ser falsos para que ela retorne falso.
Na matemática a função OU seria a união entre dois grupos. No caso qualquer valor que pertencem aos grupos fazem parte da união.
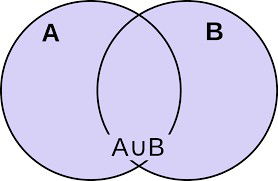
Na tabela verdade a união é vista desta forma:
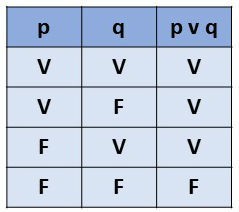
No Excel:
=OU(argumento 1; argumento 2; argumento 3; ...)
Exercício
.Identificar os alunos que possuem a nota 1 ou nota 2 acima de 7.
| Nome | Nota 1 | Nota 2 |
|---|---|---|
| Caio Mansera | 7,5 | 7 |
| Raul Guedes | 8 | 7,4 |
| Antônia Orsolato | 6 | 7 |
| Quênia Rhuby | 6 | 5 |
| Fábio Souza | 10 | 3 |
| Danielle Farrine | 4 | 4,5 |
| Edivaldo Chopp | 8 | 5 |
| Césas Alfeir | 6 | 7 |
| Paschoal Ranieri | 4,5 | 6,5 |
Solução
=OU(B2>7;C2>7)
A função SE alinhada com OU
Exercício
.Existe duas notas de cada aluno. Deverá ser identificado aqueles que tiverem pelo menos uma das notas acima de 7, com a mensagem "Aprovado"; caso as duas notas forem igual ou inferior a 7, deverá ser apresentada a mensagem "Exame".
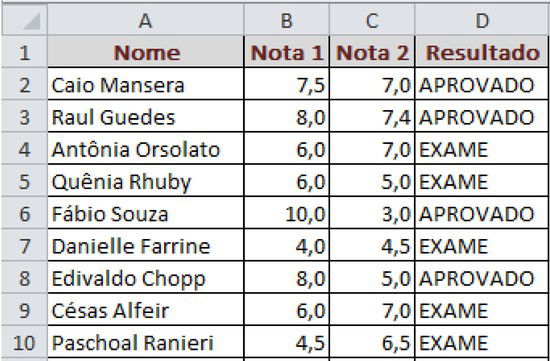
Solução
=SE(OU(B2>7;C2>7);"APROVADO";"EXAME")
A função SE alinhada com E
Exercício
Em uma planilha referente ao RH de uma empresa, você terá que identificar as pessoas solteiras, maiores de 21 anos como "grupo 1"; casadas maiores de 21 anos como "grupo 2"; e caso não satisfaça as condições mencionadas, será exibida a mensagem "Não classificada".
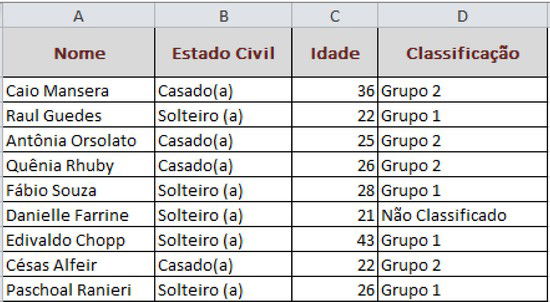
Solução
=SE( E(B2="Solteiro (a)"; C2>21); "Grupo 1"; SE( E( B2="Casado(a)"; C2 > 21); "Grupo 2"; "Não classificado"))
Mais um exemplo
Exercício
Caso um vendedor consiga vender mais que R$ 125.000,00 em mercadorias, ele ganhará um bônus de 12% do valor da venda. Mas, como na região Sul existe menos movimento, aceitou-se que, caso o vendedor reside na região Sul, ele ganhará o bônus se vender mais que R$ 100.000,00 em vendas.
| Vendedor | Região | Vendas |
|---|---|---|
| Vendedor 1 | Sul | R$ 87.925,00 |
| Vendedor 2 | Norte | R$ 129.887,00 |
| Vendedor 3 | Sudeste | R$ 12.908,00 |
| Vendedor 4 | Sul | R$ 99.087,00 |
| Vendedor 5 | Nordeste | R$ 234.987,00 |
| Vendedor 6 | Norte | R$ 10.000,00 |
| Vendedor 7 | Sul | R$ 105.000,00 |
| Vendedor 8 | Centro-Oeste | R$ 1.876.098,00 |
| Vendedor 9 | Nordeste | R$ 12.387,00 |
| Vendedor 10 | Sul | R$ 12.876,00 |
| Vendedor 11 | Sudeste | R$ 123.865,00 |
| Vendedor 12 | Centro-Oeste | R$ 128.543,00 |
| Vendedor 13 | Norte | R$ 987.000,00 |
Solução
=SE( OU( C2 > 125000; E( B2 = "Sul"; C2 >= 100000)); C2 * 0,12; "Sem bônus")
Exercícios
1. Dada a nota de um aluno na célula A1 e o número de faltas na célula B1, escreva uma fórmula que:
- Retorne "Aprovado" se a nota for maior ou igual a 7 e o número de faltas for menor ou igual a 5.
- Retorne "Recuperação" se a nota for maior ou igual a 5 e o número de faltas for menor ou igual a 5.
- Retorne "Reprovado" caso contrário.
2. Dados os valores nas células: A1 (Renda Mensal); B1 (Score de Crédito); e C1 (Possui Restrições no Nome: "Sim" ou "Não"). Escreva uma fórmula que:
- Retorne "Aprovado" se a renda for maior que 3000, o score for maior que 700 e não houver restrições no nome.
- Retorne "Análise Manual" se a renda for maior que 2000, o score for maior que 600 e não houver restrições no nome.
- Retorne "Reprovado" caso contrário.
3. Dados os valores nas células: A1 (Preço do Produto); B1 (Categoria: "Eletrônico", "Vestuário", "Alimento"); e C1 (Estoque: "Disponível" ou "Esgotado"). Escreva uma fórmula que:
- Retorne "Promoção" se o produto for da categoria "Eletrônico", o preço for maior que 1000 e estiver disponível.
- Retorne "Desconto" se o produto for da categoria "Vestuário", o preço for maior que 100 e estiver disponível.
- Retorne "Fora de Estoque" se o produto estiver esgotado.
- Retorne "Preço Normal" caso contrário.
4. Dados os valores nas células: A1 (Valor Gasto pelo Cliente); B1 (Frequência de Compra: "Alta", "Média", "Baixa"); e C1 (Tempo de Cliente: "Novo", "Antigo"). Escreva uma fórmula que:
- Retorne "Cliente VIP" se o valor gasto for maior que 1000, a frequência for "Alta" e o tempo de cliente for "Antigo".
- Retorne "Cliente Premium" se o valor gasto for maior que 500, a frequência for "Média" ou "Alta" e o tempo de cliente for "Antigo".
- Retorne "Cliente Regular" caso contrário.
5. Dados os valores nas células: A1 (Idade); B1 (Tempo de Contribuição); e C1 (Gênero: "Masculino" ou "Feminino"). Escreva uma fórmula que:
- Retorne "Aposentadoria Aprovada" se a idade for maior ou igual a 65 (homens) ou 60 (mulheres) e o tempo de contribuição for maior ou igual a 35 anos.
- Retorne "Aposentadoria Parcial" se a idade for maior ou igual a 60 (homens) ou 55 (mulheres) e o tempo de contribuição for maior ou igual a 30 anos.
- Retorne "Não Elegível" caso contrário.
6. Clique aqui para acessar a planilha dos próximos exercícios.
a) Calcule a nota bimestral de cada aluno, com elas podendo ter valores entre 0 e 10. Prova possui peso 7,5 e trabalho tem peso 2,5.
b) Nos oito dias de aula, qual aluno faltou todas as aulas? E qual aluno esteve presente em todas?
c) A média para passar é 5, quais alunos irão passar? Informe pela planilha com os dizeres "Passou" e "Não passou"
d) Imagina que o professor vai por de recuperação os alunos que faltaram mais de 3 vezes e tiveram média abaixo de 5. Quais alunos vão entrar de recuperação? Informe na planilha com os dizeres "Recuperação", "Não recuperação".
e) Se o aluno faltar mais de 6 vezes, a menos que ele tire nota acima de 9, ele irá para recuperação. Quais alunos entram nesse caso? Informe com "Caso especial de recuperação" na planilha.
7. Dado um ano na célula A1, escreva uma fórmula usando SE aninhados para verificar se o ano é bissexto. Se for bissexto, retorne "Bissexto"; caso contrário, retorne "Não é bissexto". (use a função RESTO)
8. (Questão desafio e nada a ver com a aula) -> Suponha que a data de nascimento de uma pessoa esteja na célula A1. Escreva uma fórmula no Excel que calcule a idade dessa pessoa com base na data atual.












— Comentários 0
, Reações 1
Seja o primeiro a comentar