Em aulas anteriores mencionamos estatística em dois momentos: quando falamos de cartas de controle em ferramentas básicas de qualidade e quando falávamos dos primórdios da qualidade
. O controle estatístico de processos (CEP) substituiu, por exemplo, a antiga inspeção de processos, sejam eles de compras, de recebimento de materiais, de conformidade do produto final, etc., por uma inspeção baseada em amostragens.
Ad
Objetivos do Controle Estatística de Processos
Originalmente, o CEP tinha como objetivo monitorar um produto ou serviço durante seu processo de produção, pois, caso apresentasse problemas, seu procedimento seria interrompido para que as falhas fossem sanadas e tudo retornasse à sua condição normal.
Atualmente, mais do que uma ferramenta estatística, o CEP é visto como uma filosofia de gerenciamento e um conjunto de técnicas e habilidades, originárias da estatística e da engenharia de produção, com vistas a garantir a estabilidade e a melhoria contínua de um processo de produção.
Assim, o CEP tem como função principal o controle e a melhoria do processo, sendo seus princípios fundamentais:
• pensar e decidir baseado em dados e fatos;
• pensar separando a causa do efeito, buscando sempre conhecer a causa fundamental dos problemas;
• reconhecer a existência da variabilidade na produção e administrá-la;
• identificar instantaneamente focos e locais de disfunção e corrigir os
problemas a tempo.
O CEP pode ser aplicado a qualquer processo. Para este fim, há um conjunto de métodos e ferramentas que podem auxiliar a aplicação, tais como: histogramas, checklists de verificação e controle, gráficos de Pareto, diagramas de causa e efeito (Ishikawa) e gráficos de controle.
Carta de Controle
Um gráfico de controle envolve registros cronológicos regulares de uma ou mais características calculadas a partir de amostras obtidas da produção. Estes valores são inseridos, pela ordem cronológica, em um gráfico que possui uma linha central e dois limites, chamados limites de
controle (inferior e superior).
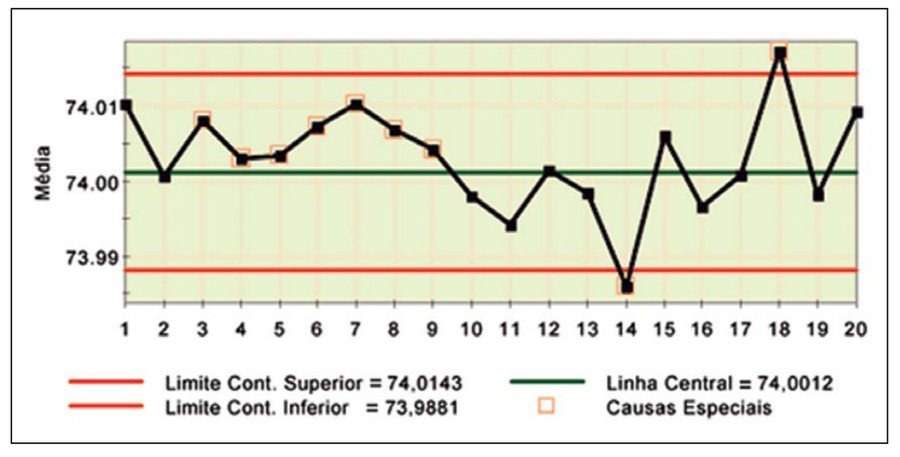
Podemos verificar que a variabilidade do processo pode se dar por causas comuns ou por causas especiais.
Causas de variação comuns
São consideradas aleatórias e inevitáveis. Quando o processo apresenta somente causas de variação comuns, as variáveis do processo seguem uma distribuição normal. Por exemplo, o peso do arroz ensacado por uma distribuidora de produtos alimentícios seguirá uma distribuição normal caso o processo apresente somente causas comuns de variação, que estejam dentro dos limites de controle.
Causas de variação especiais
Ocorrem por motivos claramente identificáveis e que podem ser eliminados. As causas especiais alteram o parâmetro do processo, média e desvio-padrão, pois estão fora dos limites de controle. Por exemplo, um equipamento cuja calibração esteja incorreta apresentará uma variação especial. Seu ajuste fará com que a variação desapareça
Como utilizar a carta de controle
Você deve estar se perguntando para que serve um gráfico de controle. A resposta é simples: verificar as causas de variação e atuar sobre elas, sempre que necessário, a fim de evitar perdas no processo produtivo. Assim, o processo de controle de variáveis deve seguir cinco fases:
1. Determinar o tipo de gráfico de controle a ser utilizado.
2. Estabelecer um plano para a retirada das amostras do que está sendo produzido.
Ad
3. Determinar os limites do gráfico de controle e da média para cada variável que será controlada.
4. Colocar os valores encontrados nos gráficos, verificando se estes valores estão nos limites do gráfico, caso em que o processo estará sobre controle.
5. Análises e situações: os resultados obtidos devem ser analisados, verificando se existe a necessidade de algum tipo de ação.
FASE I – Determinar o tipo de gráfico de controle a ser utilizado
Existem dois tipos básicos de gráficos de controle.
Gráfico de variáveis quantitativas
São utilizados quando as amostras podem ser representadas por unidades quantitativas de medida (peso, altura, comprimento, etc.). Os mais conhecidos são os gráficos da média e da amplitude (X e R), da média e desvio padrão (X e σ) e de valores individuais e da amplitude (X, R).
• (X e R): são os gráficos da média e da amplitude. São os mais usados. Os gráficos de média e de amplitude se complementam, devendo ser implementados simultaneamente. O gráfico objetiva controlar a variabilidade no nível médio do processo e qualquer mudança que ocorra nele. É
muito importante também verificar a dispersão de um processo que pode sofrer alterações devido às causas assinaláveis. Este aumento da variabilidade será detectado pelo gráfico R das amplitudes. Neste caso, estamos falando especificamente das variações especiais, como por exemplo um equipamento desregulado.
• (X e σ): são os gráficos da média e do desvio-padrão. São uma opção para os gráficos de média e amplitude e mais à frente aprenderemos a calculá-los e interpretá-los.
• (X, R): gráficos de valores individuais e da amplitude. Em alguns casos, pode ser mais conveniente controlar o processo baseado em leituras individuais do que em amostras. Isto ocorre particularmente quando a inspeção e a medida são caras, o ensaio for destrutivo ou
quando a característica que está sendo examinada for relativamente homogênea (tal como o pH de uma solução química).
Gráfico de variáveis qualitativas
são utilizados quando existem situações em que as características da qualidade não podem ser medidas numericamente. Por exemplo, uma lâmpada é classificada como “funciona” ou “não funciona”. Ou seja, existem casos em que as características da qualidade são mais bem representadas pela presença ou ausência de um atributo, e não por alguma medição. Os mais conhecidos são:
• gráficos de p: para o controle da proporção de unidades defeituosas em cada amostra;
• gráficos de np: para o controle do número de unidades defeituosas por amostra;
• gráficos de c: para o controle do número de defeitos por amostra;
• gráficos de u: para o controle do número de defeitos por unidade de produto.
Outro exemplo é utilizar parâmetros de outras empresas para averiguar a situação de um produto. Por exemplo, verificar a classificação de um banco sobre investir em uma certa empresa: "não investir", "investir com cautela", "investir".
FASE II – Estabelecer um plano para a retirada das amostras do que está sendo produzido
Ad
Antes de se realizar a coleta de dados, é necessário escolher o tamanho da amostra, também chamada de subgrupos racionais, assim como a frequência da amostragem e o número de amostras a serem coletadas.
Na amostragem, é fundamental escolher amostras que representem subgrupos de itens que sejam o mais homogêneo possível, visando ressaltar diferenças entre os subgrupos. Isso objetiva, caso estejam presentes, fazer com que as causas especiais se manifestem pelas diferenças entre os subgrupos. A busca aqui é pela eliminação do viés na amostragem.
Preste atenção neste exemplo: imagine que você deseje realizar uma pesquisa sobre a intenção de votos para o governo do estado do Rio de Janeiro. Você buscaria entrevistar pessoas de um único bairro? De uma única faixa etária? Certamente não, pois esta mostra não representaria toda a população e certamente seus dados estariam enviesados. Com a amostragem de que estamos falando aqui é a mesma coisa, temos que buscar amostras que representem cada subgrupo. Chamamos de amostras representativas. Por exemplo, não podemos pegar amostras somente de uma máquina, nem somente de um turno de trabalho.
FASE III - Determinar os limites do gráfico de controle
Os limites serão calculados como se estivéssemos calculados outliers. Fizemos uma aula bem aqui sobre o que significa outlier e como calcular.
Existe um padrão para identificar se algo é outlier, isto é, algo fora da reta. Geralmente verificamos se a probabilidade daquilo acontecer é extremamente baixa. O critério para "extremamente baixo" é se a probabilidade de ocorrer é menor que 0,1%.
De acordo com a regra da Distribuição normal, para algo ter menos de 0,1% de chance de ocorrer ele tem que estar a 3 desvios padrões distantes da média.
Assim os limites serão calculados do seguinte jeito: o limite superior será a média mais 3 vezes o desvio padrão; o limite inferior será a média menos 3 vezes o desvio padrão.
Caso com amostragem com média
Caso você saiba a probabilidade de algo, como por exemplo, ser um produto defeito. Seu desvio padrão (σ) em uma amostragem (n) se dará pela seguinte fórmula (utilizando a Distribuição Binomial):
\[ σ =\sqrt{np(1-p)} \]
E sua média será p*n.
Isto é, se um produto tem 10% de chance de ser defeituoso e você fará uma amostragem com 100 unidades. Em média, você achará 10% de 100 produtos defeituosos, isto é, 10 produtos defeituosos. E o desvio padrão será:
\[ σ =\sqrt{100 · 10% · (1 - 10%)} \]
\[ σ =\sqrt{10 · 90%} \]
\[ σ =\sqrt{9} \]
\[ σ =3 \]
Então como faríamos a carta de controle para esta amostra?
\[ \text{Limite superior} = \overline{x} + 3 * σ \]
\[ \text{Limite superior} = 10 + 3 * 3 \]
\[ \text{Limite superior} = 19 \]
Isso significa que já é espera produtos com defeitos. Mas só nos preocuparemos mesmo com o equipamento após encontrar mais de 19 produtos com defeitos em uma amostra com 100.
Ad
\[ \text{Limite inferior} = \overline{x} - 3 * σ \]
\[ \text{Limite inferior} = 9 - 3 * 3 \]
\[ \text{Limite inferior} = 1 \]
O mesmo pensamento com o limite inferior. Só nos preocuparemos se houve algum problema caso tenha menos de 1 produto com defeito.
Essas duas situações (ter mais de 19 produtos com defeitos ou ter menos de 1) é tão única e difícil de ocorrer (menos de 0,1%) que provavelmente a máquina não está regulada da forma correta.
Caso com amostragem com probabilidade
O desvio padrão (σ) neste caso muda ligeiramente. Já que o objetivo não é calcular a quantidade de peças defeituosas e sim a probabilidade de achar peças defeituosas dentro da amostra.
Neste caso lembre-se que quanto maior sua amostra, menor o desvio-padrão em relação à média, já que tudo tenderá para a média (Teorema do limite central). Conforme a Distribuição T-Student:
\[ σ =\sqrt{\frac{p(1-p)}{n}} \]
Recalcular agora os limites superiores e inferiores.
Com variáveis qualitativas
Em situações qualitativas, o critério para criar limites superiores e inferiores deve ser discutido com a equipe.
Fase IV: Análise e estabilidade dos limites
A estabilidade diz respeito à verificação da variabilidade do processo quanto a seu comportamento normal (se está ou não dentro dos limites de controle, por exemplo).
Um processo é considerado estável quando os seus gráficos de controle não indicarem sinais de anormalidade ou presença de causas especiais. Desta forma, os processos sob controle apresentam gráficos “bem comportados”, seguindo um padrão já conhecido.
Para verificação da estabilidade do processo sempre devem ser analisados os pares de gráficos (da média e da amplitude, ou da média e do desvio-padrão) em busca de sinais de anormalidade.
A características de um padrão natural, estável, de um gráfico decontrole podem ser resumidas em:
• a maioria dos pontos está próxima da linha média (cerca de 68% no intervalo de ±1σ em torno da média) sem no entanto existir concentração excessiva neste intervalo, onde “σ” é o desvio-padrão;
• cerca de 95% dos pontos (19 em 20 pontos) estão contidos no intervalo ±2 σ em torno da média;
• nenhum ponto cai fora dos limites de controle (pois a sua probabilidade é de apenas 0,27%);
• os pontos vão se distribuindo mais ou menos igualmente acima e abaixo da média;
• não se configuram tendências de aumento ou de diminuição sistemática. Por exemplo, a probabilidade de ocorrência de sete
pontos consecutivos acima da média é de 0,78 %. Logo, quando isto ocorrer, interpreta-se como uma tendência ao aumento
da média;
• não existem oscilações cíclicas
Conclusão
Controle de processos nos possibilita tomar ações corretivas antes que haja desvios que possam causar custos de retrabalho, refugo ou outros tipos de perdas.
Tenha sempre em mente que não há outra forma de se alcançar maior produtividade, menores custos e consequentemente maiores margens de lucro, se não tivermos os processos produtivos sob controle, ou seja, sem que haja causas especiais. Caso estas existam, caberá a você, futuro engenheiro de produção, aplicar seus conhecimentos para eliminá-las.
Ad
Não se esqueça de que não é necessário termos pontos fora dos limites de controle para termos que agir sob o processo. Lembre-se, por exemplo, que um processo que segue uma tendência em direção aos limites inferior ou superior já indica que precisa de intervenção. Em outras palavras, quando vemos que há um carro parado à frente, não esperamos a colisão para tomar providências. Freamos ou desviamos para evitar o impacto, ou seja, a ação corretiva foi tomada antes de o evento se tornar efetivamente um problema.
Exercícios
1) Em um processo de fabricação de um papel higiênico, cada rolo deve ter 30 metros. A máquina de corte opera com média de 30 metros, mas de vez quando deixa o rolo um pouco maior ou um pouco menor. O desvio padrão para amostras de 50 unidades calculado é de 30 centímetros. Calcule os limites superiores e inferiores. Para quais valores a seguir você deve parar a produção para checar a máquina: 30,63 metros; 29,85 metros; 29,06 metros; 30,89 metros.
2) Há 5% de probabilidade de um produto estar defeituoso. Você retira amostras de 100 unidades para verificar o estado do maquinário. Quais são os limites superiores e inferiores?







— Comments0
Be the first to comment