Curso
Capacitar o aluno no uso de técnicas estatísticas básicas para a análise exploratória de dados. Apresentar problemas que envolvam o uso da análise estatística de dados nas decisões.
Para o aluno:
- BUSSAB, Wilton de O.; MORETTIN, Pedro A. Estatística básica. Saraiva, 2017.
- Presença será cobrada;
- Haverá teste e prova.
Estatística
Relembrando, a estatística tem como objetivo a coleta, redução, análise e modelagem dos dados. De agora em diante, iremos focar bastante na modelagem dos dados. Um modelo estatístico é uma representação simplificada da realidade.
Ad
Como diria:
“Essencialmente, todos os modelos estão errados, mas alguns são úteis”
- George E. P. Box
Quando dizemos que uma moeda ao cair tem 50% de chance de ser par e 50% de chance de ser ímpar estamos criando um modelo matemático/estatístico que nos ajuda a entender esse fenômeno, nos auxiliando para uma tomada de decisão. Se parar para pensar, talvez a moeda caia em pé (ou talvez nem chegue a cair), estas n possibilidades são descartadas afim de se ter um modelo útil e compreensível.
Um modelo muito usado na biologia para estimar a quantidade de população de uma espécie é o estimador de Lincoln-Petersen. Neste modelo terá que seguir alguns passos: capture alguns indivíduos, marque-os, espere um tempo, capture de novo alguns indivíduos. No final temos a seguinte regra de 3:
Primeira captura -------- População total
Marcados achados na segunda captura -------- Segunda captura
Os animais capturados primeiramente são marcados. Logo depois há uma segunda captura e verifica-se quantos dos capturados tem as marcas, o número achado é proporcional à população total. Dados que sabemos o quanto capturamos na primeira e segunda vez, podemos fazer uma regra de 3 para saber a população total. Pronto, está descrito um modelo.
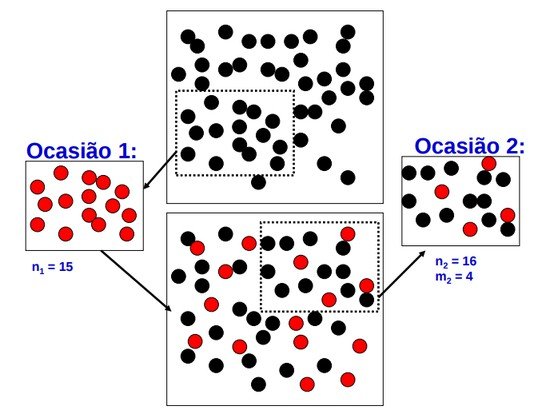
O estimador de Lincoln-Petersen tem diversas resalvas(fica como exercício pensar quais são), mas de fato é útil e o resultado final quase sempre está perto do resultado verdadeiro!
O problema aqui está no uso do quase sempre, como se espera uma informação que seja assimilada igualmente a todos, esses termos podem gerar dúvida.
- O que é quase sempre para você?
- Será que em todas as situação a chance estar perto do resultado é a mesma?
- O que é perto do resultado?
Para haver uma uniformidade no método científico não se caracteriza modelos usando palavras abstratas e sim probabilidade! Mudando a afirmação para:
>O modelo prevê uma significância de 1%
ou:
>o modelo prevê que em 99% dos casos haverá um erro menor de 5%
Probabilidade
O estudo da probabilidade começou com a vontade do homem de prever o futuro, desde os romanos realizando formações de batalhas até indagações se a astrologia realmente teria algum significado. Cícero, ao ver o exército romano de Canas ser trucidado por um exército menor de Aníbal, ironizou: "todos os romanos que caíram em Canas teriam, por acaso, o mesmo horóscopo?". Cícero foi o criador do termo probabilis, que acabou por originar a palavra probabilidade. [2]
Os romanos também criaram o Digesto, uma seção do código de leis romanas, compilado pelo imperador Justiniano no século VI, o primeiro documento no qual a probabilidade aparece como figura jurídica. Anteriormente os conflitos jurídicos eram resolvidos na força, escolhendo um homem para lutar em seu lugar. Ao substituírem esse método antigo, utilizou-se o conceito de provas e testemunhas, ao final, preocupavam-se com a probabilidade da verdade estar sendo dita ser a maior. [2]
Ad
Mas, por que anteriormente aos romanos não haviam estudos na área da probabilidade?
> Por que os gregos não desenvolveram uma teoria das probabilidades? Uma resposta é que muitos gregos acreditavam que o futuro se desvelava conforme a vontade dos deuses. Se o resultado de um jogo de astrágalos significava “casa-te com a espartana atarracada que te imobilizou naquela luta atrás do quartel”, um rapaz grego não veria o jogo como um produto da sorte (ou azar) num processo aleatório; ele o veria como a vontade dos deuses. Com essa visão de mundo, um entendimento da aleatoriedade seria irrelevante. Portanto, a previsão matemática da aleatoriedade teria parecido impossível. [2]
A vontade dos deuses não é a única explicação plausível. A falta de interesse no estudo da probabilidade também pode ser explicado pelos viéses heurísticos que lidamos diariamente.
A heurística da disponibilidade, relacionada à tendência do indivíduo em recorrer as suas
últimas lembranças ou experiências, facilmente captadas da memória. Isso ocorre devido a quando reconstruirmos o passado damos uma importância injustificada às memórias mais vívidas. Como exemplo, quantos palavras de 6 letras a 4º letra é ç? E quantas palavras de 6 letras terminam com ção? Se você acredita que existem mais palavras que terminam com ção do que tem a 4º letra ç você caiu na heurística da disponibilidade. [1]
A heurística da representatividade baseia-se na utilização dos modelos mentais de
referência (estereótipos) como base para a tomada de decisão. Casos de preconceito, racismo ou "situações desconfortáveis", como do brasileiro Jean Charles de Menezes, morto em 2005 por ter sido confundido por um terrorista, são claros exemplos de como essa heurística podem afetar nossas decisões. [1]
Já a heurística da ancoragem é um viés cognitivo que descreve a comum tendência humana de se "ancorar" a uma característica ou parte da informação recebida. Para comprovar o efeito ancoragem, há uma simulação onde pessoas escrevem seu dois últimos números do CPF em um papel. Logo após, o orientador cria um cenário em que a pessoa deve dar de presente um charuto a outra qualquer e escrever o valor que pagaria pelo mesmo ao lado dos números do CPF. O resultado comprova que: quanto maior o número do CPF da pessoa, a tendência é de que maior será o valor agregado ao charuto. A explicação se dá pelo simples fato de muitas pessoas não terem a ancoragem de um charuto na sua vivência e mesmo assim inconscientemente o cérebro busca através de uma ancoragem, a resposta para o preço do charuto. Como o número do CPF é a única ancoragem dada ao cérebro, ele se baseia nela para dar a resposta. [3]
O quadro abaixo demonstra as heurísticas que vivemos diariamente.
| Heurística | Viés |
|---|---|
| Disponibilidade | Facilidade de lembrança Associações pressupostas Recuperabilidade |
| Representatividade | Insensibilidade aos índices básicos Interpretação errada da chance Regressão à média interpretação errada da chance falácia da conjunção |
| Ancoragem e ajuste | Excesso de confiança Armadilha da confirmação Maldição do conhecimento |
Ad
O problema de Monty Hall
O jogo, de 1970, consiste no seguinte: Monty Hall (o apresentador) apresentava três portas aos concorrentes, sabendo que atrás de uma delas está um carro (prêmio bom) e que as outras têm prêmios de pouco valor, imagina-se uma cabra atrás de cada outra porta. [4]
- Na 1.ª etapa o concorrente escolhe uma das três portas (que ainda não é aberta);
- Na 2.ª etapa, Monty abre uma das outras duas portas que o concorrente não escolheu, revelando que o carro não se encontra nessa porta;
- Na 3.ª etapa Monty pergunta ao concorrente se quer decidir permanecer com a porta que escolheu no início do jogo e abre-a ou se muda para a outra porta que ainda está fechada para então a abrir. Agora, com duas portas apenas para escolher — pois uma delas já se viu, na 2.ª etapa, que não tinha o prêmio — e sabendo que o carro está atrás de uma das duas, o concorrente tem que tomar a decisão.
Escolher a outra porta ou manter-se na mesma? O paradoxo de Monty Hall é de menos de 50 anos atrás, mas foi um dos casos mais comentados no campo da estatística. Inspirado pelo programa Let's Make a Deal da mesma época, ficou extremamente famoso nos EUA e a pessoa que o respondeu foi Marilyn vos Savant, famosa por ser citada há muitos anos no Hall da Fama do Livro Guinness dos recordes como a pessoa com o maior QI já registrado no planeta (228). Marilyn afirmou que é vantajoso escolher outra porta, onde gerou uma avanlache de cartas onde mais de 92% do público americano dizia que ela estava errada!
Marylin está certa, o que gerou a frase:
> Nosso cérebro não foi muito bem projetado para resolver problemas de probabilidade
Trabalho para pensar
- Algum viés já influenciou suas opiniões?
- Pense em modelos que podemos criar para situações ocorrentes na nossa vida.
Conclusão
O curso pretende apresentar modelos e situações de probabilidade de nossa vida real. Atente-se bastante às falhas dos modelos, às falhas que pesssoas tem apenas por serem pessoas, podendo ocorrer na coleta, análise e inferência dos dados. Lembre-se que a partir de agora estamos no campo da ciência e o linguajar por esse motivo muda. Não use termos abstratos, use termos universais!
Referências
[1] JUNIOR, Willian Gatti; NASCIMENTO, Paulo Tromboni de Souza. Heurísticas e vieses aplicados à gestão do relacionamento com fornecedores: Uma contribuição à teoria de operações comportamentais. XVIII SIMPEP–Simpósio de Engenharia de Produção. Bauru–SP: Nov, 2011.
[2] MLODINOW, Leonard. O andar do bêbado. Zahar, 2009.
[3] Aronson, E. et al. (2003). Sozialpsychologie. Pearson Studium. ISBN 3827370841
[4] https://pt.wikipedia.org/wiki/Problema_de_Monty_Hall







— commentaires0
Soyez le premier à commenter