Introdução
Ao longo das aulas passadas, foi estudado variáveis aleatória discretas, onde adaptam-se muito bem a uma série de problemas práticos. Para algumas dessas distribuições, existem tabelas e gráficos que facilitam o cálculo e a passagem de informação sobre seus parâmetros.
Modelos probabilísticos para variáveis aleatórias discretas
Distribuição Uniforme discreta
Esse é o caso mais simples de variável aleatória onde cada valor possível ocorre com a mesma probabilidade.
\[ P(X = x_i) = p(x_i) = p = \frac{1}{k}\]
Ad
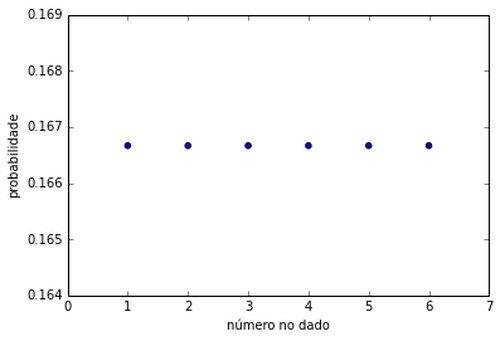
Como exemplo, qual a probabilidade de cada número ao lançar um dado?
| Número no dado | Probabilidade |
|---|---|
| 1 | 1/6 |
| 2 | 1/6 |
| 3 | 1/6 |
| 4 | 1/6 |
| 5 | 1/6 |
| 6 | 1/6 |
Ou graficamente:
Distribuição de Bernoulli
A distribuição de bernoulli, nome em homenagem ao cientista suíço Jakob Bernoulli, representa uma escolha. São experimentos tais que os resultados apresentam ou não uma determinada característica. Exemplo:
- Uma moeda é lançada: o resultado pode ser cara ou não(ocorrendo, então, coroa).
- Um dado é lançado: ou ocorre face 5 ou não(ocorrendo então as outras face possíveis)
- uma peça é escolhida ao acaso de um lote contendo 500 peças: essa peça é defeituosa ou não;
- uma pessoa escolhida ao acaso dentre 1.000 é ou não do sexo masculino;
- uma pessoa é escolhida ao acaso entre os moradores de uma cidade e verifica-se se ela é favorável ou não a um projeto municipal.
Para cada experimento há uma ocorrência de sucesso (valor 1) ou fracasso (valor 0).
Assumimos como p a probabilidade de ocorrer sucesso. Assim:
\[ p(1) = P(X = 1) = p \]
\[ p(0) = P(X = 0) = 1 - p \]
Percebe-se que se a probabilidade de sucesso é p, a probabilidade de fracasso é 1 - p.
A variância para esse caso será a diferença entre o todo menos a media:
\[ Var(x) = (p - 0) · (1 - p) + p · (p - p) = p · (1 - p) \]
A notação para um ensaio de Bernoulli é o seguinte:
\[ X \sim Ber(p) \]
Distribuição binomial
Ao repetir o ensaio de Bernoulli n vezes, ou, de maneira alternativa, ter obtido uma amostra de tamanho n de uma distribuição de Bernoulli, uma amostra particular será constituída de uma sequência de sucessos e fracassos; supondo que essas repetições sejam independentes, isto é, o resultado de um ensaio não interfere no resultado de outro. Essa repetição pode ser modelada a partir da distribuição binomial. Em resumo, ela necessita das seguintes caractéristicas:
a. O experimento deve ser repetido, nas mesmas condições, um número finito de vezes (n).
b. As provas repetidas devem ser independentes, isto é, o resultado de uma não deve afetar os resultados das sucessivas.
c. Em cada prova deve aparecer um dos dois possíveis resultados: sucesso e insucesso.
d. No decorrer do experimento, a probabilidade p do sucesso e a probabilidade q (q = 1- p) do insucesso manter-se-ão constantes.
Pode-se encontrar as seguintes situações com essas características:
- uma moeda é lançada três vezes; qual é a probabilidade de se obter duas caras?
- um dado é lançado cinco vezes; qual é a probabilidade de se obter face 5 no máximo três vezes?
- dez peças são extraídas, ao acaso, com reposição, de um lote contendo 500 peças; qual é a probabilidade de que todas sejam defeituosas, sabendo-se que 10% das peças do lote são defeituosas?
Ad
- cinco pessoas são escolhidas ao acaso entre 1.000; qual é a probabilidade de que duas sejam do sexo masculino?
- sabe-se que 90% das pessoas de uma cidade são favoráveis a um projeto municipal. Escolhendo-se 100 pessoas ao acaso entre os moradores, qual é a probabilidade de que pelo menos 80 sejam favoráveis ao projeto?
Observe que nos dois últimos casos, o fato de estarmos extraindo indivíduos de um conjunto muito grande implica que podemos supor que as extrações sejam praticamente independentes. Caso o conjunto seja pequeno, esses dados deveriam ser tratado por outra distribuição: a distribuição hipergeométrica
Uma característica interessante das situações consideradas é que há interesse apenas no número total de sucessos e não na ordem em que eles ocorrem. A probabilidade de ocorrer uma sequência com k sucessos em uma amostra de tamanho n é:
\[ \text{Probabilidade de dar sucesso: }p^{k} \]
\[ \text{Probabilidade de dar fracasso: }(1 - p)^{n - k} \]
\[ \text{Probabilidade de ocorrer uma sequência com k sucessos: }p^{k} * (1 - p)^{n - k} \]
Resta saber quantas sequências com a propriedade especificada podemos formar. É fácil ver por combinação simples que existem:
\[ \binom{n}{k} = \frac{n!}{k!(n-k)!} \]
Consequentemente:
\[ \text{Probabilidade de ocorrer k sucessos: }P(X = k) = \binom{n}{k} p^{k} (1 - p)^{n - k} \]
Com a seguinte notação:
\[ X \sim B(n, p) \]
Exemplos
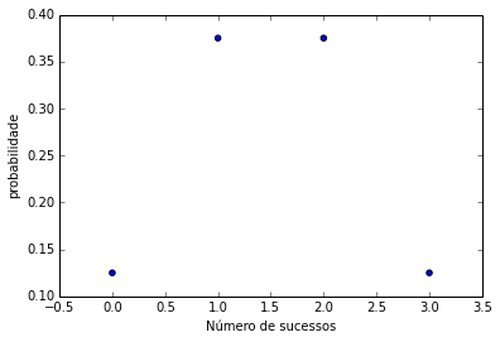
Exemplo 1: uma moeda é lançada três vezes; qual é a probabilidade de se obter duas caras?
Pela fórmula, podemos obter a seguinte tabela:
| Nº de sucessos | Probabilidade | p = 1/2 |
|---|---|---|
| 0 | q³ | 1/8 |
| 1 | 3pq³ | 3/8 |
| 2 | 3p²q | 3/8 |
| 3 | p³ | 1/8 |
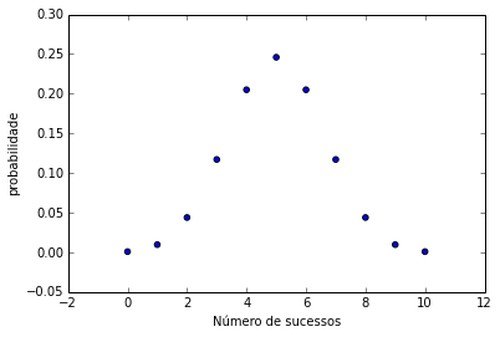
Exemplo 2: dez peças são extraídas ao acaso de um lote. Monte a tabela de probabilidade de sucessos se 50% das peças do lote são defeituosas.
Pela fórmula, podemos obter a seguinte tabela:
| Nº de sucessos | Probabilidade | p = 50% |
|---|---|---|
| 0 | q¹⁰ | 0,09% |
| 1 | 10pq⁹ | 0,97% |
| 2 | 45p²q⁸ | 4,39% |
| 3 | 120p³q⁷ | 11,71% |
| 4 | 210p⁴q⁶ | 20,50% |
| 5 | 252p⁵q⁵ | 24,60% |
| 6 | 210p⁶q⁴ | 20,50% |
| 7 | 120p⁷q³ | 11,71% |
| 8 | 45p⁸q² | 4,39% |
| 9 | 10p⁹q | 0,97% |
| 10 | p¹⁰ | 0,09% |
Exemplo3: 200 peças são extraídas ao acaso de um lote. Monte o gráfico de probabilidade de sucessos se 50% das peças do lote são defeituosas.
Ad
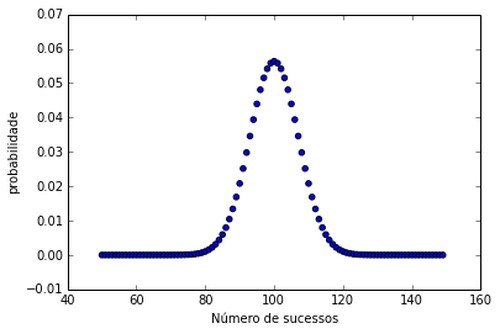
Percebe-se que quanto mais amostra acrescentamos ao problema, mais a distribuição parece ganhar forma!
Essa análise fez a estatística chegar ao seguinte teorema.
Teorema central do limite
“Quando o tamanho da amostra aumenta, a distribuição amostral da sua média aproxima-se cada vez mais de uma distribuição normal.”
- Teorema Central do Limite
Mas afinal, o que é uma distribuição normal?
Modelos probabilísticos para variáveis contínuas
Quando trabalha-se com variáveis contínuas, é assumido que há uma infinidade de possíveis eventos. Como exemplo, a altura de um ser humano pode ser: 1,6 ou 1,61 ou 1,612 ou 1,6125 ou 1,61256 etc...
Como a probabilidade de um evento é a ocorrência dele sobre o total, a probabilidade de um certo evento contínuo sempre será zero, porque:
\[ \text{Probabilidade de certo evento contínuo: } \frac{\text{ocorrências desse evento}}{\text{soma de todas as ocorrências}} = \frac{\text{ocorrências desse evento}}{\text{infinito}} = 0 \]
Para trabalhar com probabilidade de variáveis contínuas normalmente considera-se períodos. Assim, se quisermos estudar a probabilidade de um ponteiro de relógio estar no minuto 2:
\[ P(2 \leq X < 3) = \frac{1}{60} \]
Através da divisão do intervalo [0, 60[ em pequenos subintervalos, podemos construir um histograma para as probabilidades da variável aleatória X.
> A probabilidade do intervalo é igual à área desse intervalo
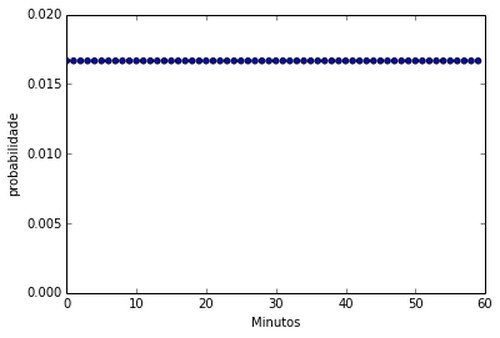
O gráfico de probabilidade conforme cada intervalo é chamado função de densidade de probabilidade (f.d.p.) da variável aleatória X.
Por exemplo, pode-se considerar o seguinte f.d.p. e pretende-se calcular dela a probabilidade de x estar entre 0 e 0.5:
\[ F(x) = 2x \text{, para } 0 \leq x \leq 1 \]
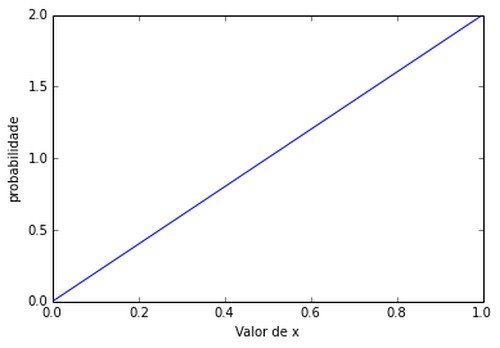
A área seria o triângulo formado pelos valores de x entre 0 e 0.5:
\[ p(0 \leq x \leq 0.5) = \frac{0.5 * 1}{2} = \frac{1}{4} = 25\% \]
O modelo Gaussiana ou normal
Suas origens remontam a Gauss em seus trabalhos sobre erros de observações astronômicas, por volta de 1810, donde o nome de distribuição gaussiana para tal modelo.
Em termos mais formais, a distribuição normal é uma distribuição de probabilidade absolutamente contínua parametrizada pela sua esperança matemática (média) e desvio padrão. Devido a isso, há uma infinidade de distribuições normais:
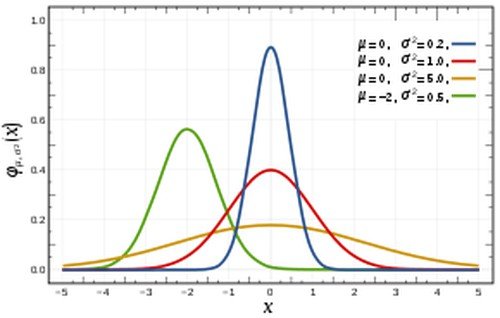
A distribuição normal com média nula e desvio padrão unitário é chamada de distribuição normal centrada e reduzida ou de distribuição normal padrão.
Como dito no teorema do limite central, tudo que pode ser considerado a soma de um grande número de pequenos valores aleatórios independentes aproxima–se de uma distribuição normal. O teorema central do limite é válido para toda distribuição de probabilidade com variáveis independentes e identicamente distribuídas e desvio padrão finito. Por exemplo:
Ad
- Se as variáveis seguem a distribuição de Bernoulli
- Se as variáveis seguem a distribuição qui–quadrado com um graus de liberdade
- Se as variáveis seguem a distribuição exponencial
Também pode ser criados processos de normalização para variáveis que não se enquadram nessas características passarem a se enquadrar.
Utilizações da Guassiana
- Balística.
No século XIX, para melhorar a precisão da artilharia de fogo muitos tiros de canhão eram disparados. Observou–se que a direção e o alcance eram semelhantes às distribuições normais.
- Quociente de inteligência
- Anatomia humana (tamanho de orelha, altura etc...)
- Anatomia animal (tamanho de um ovo)
- Economia (preço de commoditie
- Sinais e medições físicas (transmissão de um sinal através de um cabo elétrico, a sua perda ou ruído tem distribuição normal)
- Etc...
Critérios para verificação de normalidade
O critério mais simples consiste em traçar um diagrama em barras da distribuição e verificar visualmente se o diagrama é em forma de sino, com simetria em relação ao centro. Entretanto, este critério subjetivo permite eliminar uma parte das distribuições quando consideradas não gaussianas. Critérios mais avançados consistem em verificar as faixas de normalidade, testes estatísticos de normalidade, cálculo de das estimativas dos parâmetros etc...







— commentaires0
Soyez le premier à commenter