O que é inferência estatística
A palavra inferência tem, para este contexto, o significado de conclusivo. Para inferência estatística, queremos obter conclusões sobre nosso conjunto de dados a partir de modelos.
A inferência estatística faz proposições sobre um universo, usando dados tirados de uma amostragem. Dada um hipótese sobre um universo, para o qual nós queremos tirar inferências, a inferência estatística consiste em (primeiramente) selecionar um modelo estatístico do processo que gera os dados e (segundamente) deduzir as proposições a partir do modelo.
Ad
Uma das ferramentas mais importantes na inferência estatística é o intervalo de confiança (IC), que fornece uma faixa de valores que provavelmente contém o parâmetro populacional verdadeiro, como a média ou a proporção. O intervalo de confiança não apenas estima o parâmetro, mas também expressa a incerteza associada a essa estimativa.
Nesta aula, exploraremos o conceito de intervalo de confiança, como ele é construído e interpretado, além de suas aplicações em diversas áreas.
Quando utilizar Intervalo de Confiança
Intervalos de confiança são usados para indicar a confiabilidade de uma estimativa. Por exemplo, um IC pode ser usado para descrever o quanto os resultados de uma pesquisa são confiáveis. Sendo todas as estimativas iguais, uma pesquisa que resulte num IC pequeno é mais confiável do que uma que resulte num IC maior.
Podemos interpretar o intervalo de confiança como um intervalo que contém os valores "plausíveis" que a média da população pode assumir. Assim, a amplitude do intervalo está associada a incerteza que temos a respeito do parâmetro.
Vamos entender esse intervalo com um exemplo: qual a média de um lançamento de um dado de 6 faces? A média é 3,5, em outras palavras, a população tem média 3,5. Agora, imagina que lançando um dado 5 vezes coletamos os seguintes dados:
\[ 1,6,3,2,1 \]
A média da amostra é 2,6!!
Agora lançamentos de novo 5 dados:
\[ 5,3,6,3,1 \]
Dessa vez a média da amostra é 3,83!!
Simulações com a média amostral
E se começarmos a guardar esse resultado da média? Vamos fazer algumas simulações:
Simulações para amostra de tamanho 5
Para 10 grupos de 5 lançamentos de dados (amostra tamanho 5)
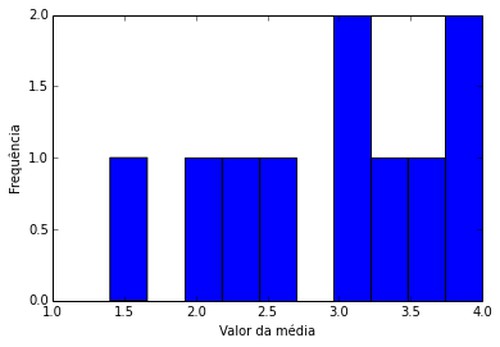
Para 30 grupos de 5 lançamentos de dados (amostra tamanho 5)
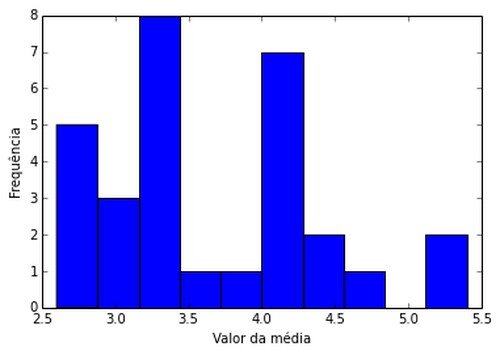
Para 70 grupos de 5 lançamentos de dados (amostra tamanho 5)
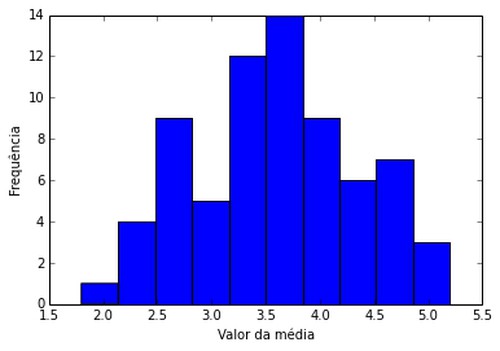
[h3]{Para 200 grupos de 5 lançamentos de dados (amostra tamanho 5)v
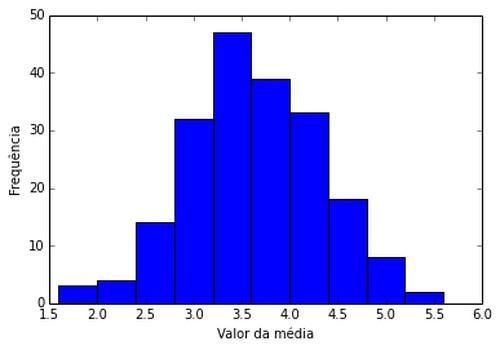
Para 2000 grupos de 5 lançamentos de dados (amostra tamanho 5)
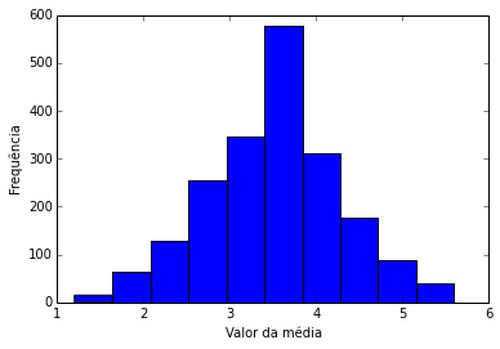
Depois de uma certa quantidade é possível verificar uma curva normal ocorrendo. Mas demorou para a curva normal aparecer, logo, vamos fazer uma mudança, e se usarmos uma amostra de tamanho 200? Isto é, vamos ver a média depois de lançar 200 dados, espera-se que a média fique em volta de 3,5 como é da população! Vamos para as simulações:
Simulações para amostra de tamanho 200
Para 10 grupos de 200 lançamentos de dados (amostra tamanho 5)
Para 70 grupos de 200 lançamentos de dados (amostra tamanho 5)
Ad
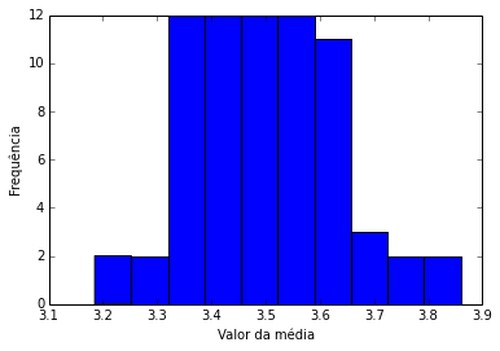
[h3]{Para 200 grupos de 200 lançamentos de dados (amostra tamanho 5)v
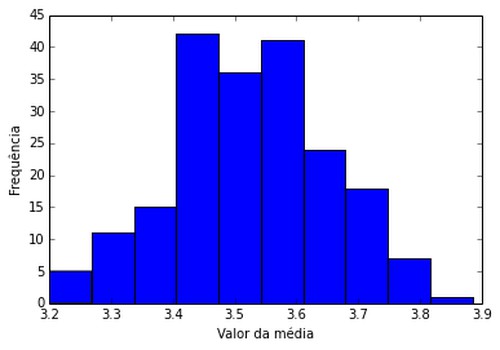
Para 2000 grupos de 200 lançamentos de dados (amostra tamanho 5)
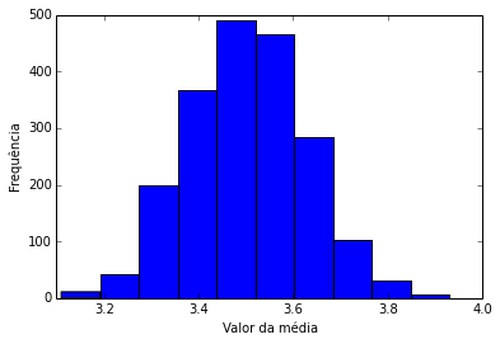
De novo o gráfico é similar a uma normal!
Conclusões sobre as simulações
Percebe-se dois pontos:
O gráfico é similar à normal. No caso usaremos a teoria central do limite de novo: Em repetidos experimentos, a média de uma amostra irá tender a uma distribuição normal.
A amplitude do primeiro é diferente da amplitude do segundo. Lidando com amostras, quanto maior sua amostra, menor o desvio padrão da média amostral.
Média amostral
Assim, dizemos que a média amostral é normalmente distribuída. A variância da média amostral é a variância da população dividida pelo tamanho da amostra:
\[ \text{Var}(\bar{X}) = \frac{\sigma^2}{n} \]
Ela é dependente da média da amostra e o desvio padrão da amostra dividido pela raiz do tamanho da amostra.
\[ \bar{X} \sim N\left(\mu, \frac{\sigma^2}{n}\right) \]
A significância no intervalo de confiança da média amostral
O tamanho do intervalo é definido pela distribuição normal da média amostral e da confiança escolhida. Por exemplo, é comum usar para estes cálculos 95% de confiança, isso quer dizer que em 95% das vezes a média da população estará neste intervalo. A confiança é inversamente proporcional à significância, a significância está ligada ao erro do teste, neste caso, uma confiança de 95% significa uma significância de 5%.
No caso, essa confiança é denominada alpha e procuramos um intervalo em que a média populacional estará abrangendo a confiança dada:
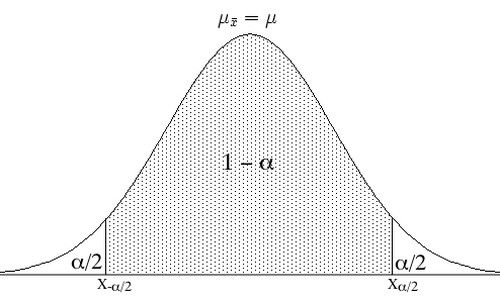
Assim, dado o nível de confiança que gostaria de ter: 90%, 95%, 98%, 99% etc... irá procurar os pontos que possibilitam ter um intervalo com essa confiança. Em intervalos bicaudais, um intervalo que tende para direita quanto para esquerda, procuramos os pontos onde deixem a probabilidade de erro metade para esquerda e metade para direita.
Exemplo real
Uma pesquisa de opinião entrevistou 2500 pessoas com respeito se irão votar ou não votar num candidato A. Em média, 20% dos entrevistados votarão no candidato A e sabemos que o desvio padrão populacional é de 40%, já que o desvio amostral é de 40% e temos uma amostra muito grande(mais de 2000 pessoas). Uma empresa de consultoria quer construir um intervalo de confiança para a média populacional, em outras palavras, poder, a partir dessa amostra, definir quantas pessoas vão votar no candidato A na população total. Para isso definiu que haverá 5% significância ou 95% de confiança seu intervalo.
Um intervalo de 95% de confiança bicaudal indica que haverá 2,5% de erro à direita e à esquerda. Sabendo que a média de uma amostra se comporta como uma normal, o Z que estabelece o erro de 2,5% à esquerda é de -1,96 e o Z que estabelece erro de 2,5% à direita é de 1,96. Em resumo:
Ad
\[ −1,96<\text{nosso intervalo na normal reduzida}<1,96 \]
No caso é na normal reduzida. Devemos assim transformá-la para a normal da questão que possui 20% de média.
\[ P(X<2,5\%)=20\%−1,96∗\frac{40\%}{√2500}=18,43\% \]
\[ P(X>97,5\%)=20\%+1,96∗\frac{40\%}{√2500}=21,56\% \]
O que aconteceria se utilizarmos os mesmos parâmetros do exercício anterior, mas 40% dos entrevistados vão votar no candidato A com desvio padrão populacional de 24%?
\[ P(X<2,5\%)=40\%−1,96∗\frac{24\%}{√2500}=39,05\% \]
\[ P(X>97,5\%)=40\%+1,96∗\frac{24\%}{√2500}=40,94\% \]
O que aconteceria se utilizarmos os mesmos parâmetros do exercício anterior, mas com significância de 2%?
Significância de 2% significa que ignoraremos os 1% de média inferiores ou os 1% maiores médias:
\[ P(X<1\%)=40\%−2,33∗\frac{24\%}{√2500}=38,88\% \]
\[ P(X>99\%)=40\%+2,33∗\frac{24\%}{√2500}=41,11\% \]
Exercícios
1) Se uma amostra aleatória n=25, tem uma média amostral de 51,3 e uma desvio padrão populacional de σ=2. Construa o intervalo com 95% de confiança para a média populacional µ.
2) Sabe-se que a vida em horas de um bulbo de lâmpada de 75W é distribuída de forma aproximadamente normal com desvio padrão de σ=25. Uma amostra aleatória de 20 bulbos tem uma vida media de 1.014 horas. Construa um intervalo de confiança de 95% para a vida média.
3) Qual deve ser o tamanho da amostra para que o intervalo com 99,5% de confiança para a média populacional tenha uma semi amplitude não superior a 1,5? Sabe-se que a variância populacional é de 23.
4) Qual deve ser o tamanho de uma amostra cujo desvio padrão é 10 para que a diferença da média amostral para a média da população, em valor absoluto, seja menor que 1, com coeficiente de confiança igual a:
a) 95%
b) 99%
5) Uma variável aleatória X tem distribuição normal, com média amostral 100 e desvio padrão populacional 10. Se o tamanho amostral é de 16 elementos, calcule P(90 < média populacional < 110).
6) Que tamanho deveria ter uma amostra com média amostral de 100 e desvio padrão populacional 10 para que P(90 < média populacional < 110) = 95%?
7) Uma amostra aleatória de 625 donas de casa revela que 70% da amostra preferem a marca A de detergente com desvio padrão populacional de 45%. Construir um intervalo de confiança para p = proporção das donas de casa que preferem A com coeficiente de confiança γ = 90%.
8) Suponha que estejamos interessados em estimar a porcentagem de consumidores de um certo produto. Se a amostra de tamanho 300 forneceu 100 indivíduos que consomem o dado produto, determine o intervalo de confiança da média populacional, com c.c. de 95%; interprete o resultado.
Gabarito
1) I.C. = 51,3 ± 0,78;
2) I.C. = 1014 ± 11;
3) 81;
4) a) 385; b) 665;
5) Quase 100%;
6) Aproximadamente 4.
7) (0.6692 ; 0.7308).
8) (0.280; 0.387).






— Comments0
Be the first to comment